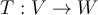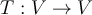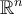Isometría p.i. ortogonalidad

Isometría p.i. ortogonalidad

de Roberto Elbio Peroni Martinez -
Número de respuestas: 2

Buenos días 

Tengo un par de consultas teóricas que creo que están relacionadas.

Una isometría es una transformación lineal que conserva el producto interno. Por lo que está asociada, por lo menos, a un producto interno  definido en el espacio vectorial donde está definida T. Mi consulta es si T termina siendo una isometría en cualquier P.I. que se tome? O sea la que es propiamente una isometría es T, independiente del p.i. que se tome. 

Y después, no es una duda propiamente, cuando hablamos de ortogonalidad asocio inevitablemente a un producto interno. Pero las matrices ortogonales escinden de tal. Es claro que es debido a la relación entre T y su matriz asociada en una, justamente, base ortonormal.  Ahora me sigue haciendo ruido, más considerando el hecho de que cualquier base se puede convertir en ortonormal definiendo un producto interno convenientemente.



En respuesta a Roberto Elbio Peroni Martinez

Re: Isometría p.i. ortogonalidad

de Florencia Cubria -
Hola Roberto.

T: V \to W T.L. es una isometría si preserva el producto interno, y "preservar el producto interno" involucra dos productos internos: el del espacio V y W, por lo tanto, ser isometría sí depende del PI considerado.

Por otro lado T:V\to V es ortogonal si T^{-1}=T^* y como la definición de T^* también depende del PI considerado, la definición de TL ortogonal sí depende del PI considerado.

Finalmente, la definición de matriz ortogonal A^{-1}={A^{t}} no depende de ningún producto interno (es una definición que está dada únicamente en términos de la inversa de la matriz y su transpuesta), aunque sí tenemos un resultado que nos indica que una matriz es ortogonal si y sólo si sus columnas conforman una BON con el PI usual de \mathbb{R}^n lo que puede llegar a confundir.

Dime si queda alguna duda.

Saludos, Florencia.