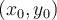CDIVV - 1S: Ejercicio 3 del apartado evaluaciones anteriores | FING

Página Principal

Ejercicio 3 del apartado evaluaciones anteriores

Hola en este ejercicio se pide taylor de orden 2 de f(x,y) = log(x² + y) en el punto (1,0).

Logré resolverlo usando la definición, pero a la hora de querer resolverlo usando la composición me queda algo distinto.

Lo que hice fue hallar taylor de orden 2 de log(x) en el punto 1, que me dio como resultado (x - 1) -(1/2!)(x-1)² y luego compuse con x² + y quedandome x² + y - 1 -(1/2!)(x² + y -1)² y al desarrollar las cuentas me queda algo totalmente distinto.

Re: Ejercicio 3 del apartado evaluaciones anteriores

de Bernardo Marenco - martes, 18 de junio de 2024, 16:12

Hola. El problema es que el resultado que se menciona en el ejercicio 2 solo vale para una composición de funciones

$h(g(x,y))$ donde la función

$g$ cumpla que

$g(x_0,y_0)=0$ , siendo

$(x_0,y_0)$ el punto en el que querés calcular el desarrollo . En este caso,

$(x_0,y_0)=(1,0)$ y

$f(x,y) = \log(x^2+y)$ la estaríamos escribiendo como

$f(x,y) = h(g(x,y))$ con

$h(x) = \log(x)$ y

$g(x,y) = x^2+y$ . Fijate que entonces

$g(x_0,y_0) = g(1,0) = 1 \neq 0$ , por lo que no podés usar el resultado de la composición.

Saludos