Buenas
Estudiando el signo de la derivada obtienes que en  tienes un minimo relativo y en
tienes un minimo relativo y en  tienes un máximo relativo.
tienes un máximo relativo.
Si te preguntaran por el máximo y el mínimo en un intervalo cerrado (que sabes que existe por Weierstrass) tendrias que evaluar la funcion en los extremos y en los puntos criticos.
Si por ejemplo te piden los extremos en el intervalo [-100,100] obtendrias que el minimo se realizar en  .
.
Como estudiar entonces cuando no es un intervalo cerrado. En este caso, como , lo que haremos es tomar un intervalo cerrado "grande" donde lo que valga
, lo que haremos es tomar un intervalo cerrado "grande" donde lo que valga  "fuera" del intervalo sea cercano a 1.
"fuera" del intervalo sea cercano a 1.
Primero observemos que  evaluado en
evaluado en  es menor que 0, mientras que en
es menor que 0, mientras que en  es mayor que 0.
es mayor que 0.
Tenemos que  . Por definicion de limite en infinito esto quiere decir que existen
. Por definicion de limite en infinito esto quiere decir que existen 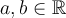 con
con 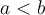 tal que
tal que
Luego el mínimo de  en [a,b] se da en
en [a,b] se da en  y para todo
y para todo ![s \notin [a,b] s \notin [a,b]](https://eva.fing.edu.uy/filter/tex/pix.php/0210061d2a08e47ae44e0f5584b4294b.png) se tiene que
se tiene que  es decir
es decir  tiene un mínimo absoluto en
tiene un mínimo absoluto en  . Lo mismo puedes hacer para el maximo
. Lo mismo puedes hacer para el maximo
Cualquier cosa vuelve a escribir
Saludos




