Buenas,
no entiendo como concluir que 
en un paso mas puedo decir que si tomo 
entonces se cumple todo?
Ya que si 
, por antecedente falso se cumple la implicancia y listo?
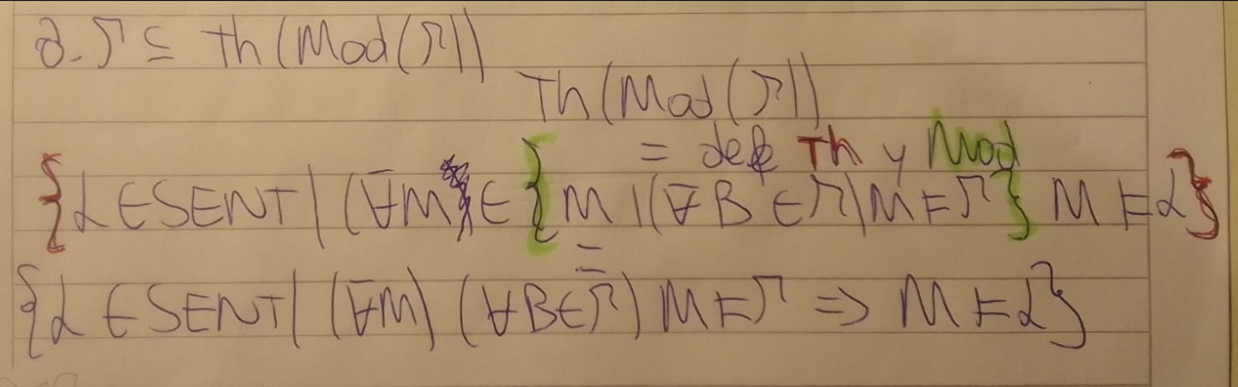
Gracias
Hola Juan:
En tu desarrollo estás expandiendo mal la definición de MOD ya que β aparece cuantificada pero no aparece en el resto de la expresión.
La expresión correcta sería:
- {α ∈ SENT / (∀M ∈ {M eta / (∀β ∈ Γ) M ⊧ β}) M ⊧ α}
Esto lo podemos simplificar un poco:
- {α ∈ SENT / (∀M eta) (M ⊧ Γ ⇒ M ⊧ α)}
Así resulta fácil de probar que las fórmulas de Γ pertenecen a ese conjunto.