Consultas del libro de ejercicio - Capítulo 7: Cálculo de integrales

Buenas

Entiendo que estas preguntando por la parte b. te comento que es la parte mas dificil, te recomiendo que hagas alguna de las otras partes antes.

Voy a ver la integral de $\sqrt{x^2 - 1}$, observa como pasar a esta con un cambio de variable lineal.

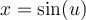Si bien se puede realizar de otras maneras, la idea aqui es hacer un cambio de variable, La idea aqui es hacer algo similar al caso de $\sqrt{1-x^2}$, en ese caso usamos como cambio de variable $x = \sin(u)$, y usando que $\sin(u)^{\prime} = \cos(u)$ y $\cos^{2}(u) + \sin^{2}(u) = 1$.

Bien en este caso usaremos las funciones hiperbolicas, $\cosh(u) = \frac{e^{x} + e^{-x}}{2}$ $\sinh(u) = \frac{e^{x} - e^{-x}}{2}$, estas funciones cumplen que $\cosh^{\prime}(u) = \sinh(u)$ $\sinh^{\prime}(u) = \cosh(u)$ y $\cosh^{2}(u) - \sinh^{2}(u) = 1$

Si realizamos el cambio de variable $x = \cosh^{2}(u), dx = \sinh^{2}(u)$ entonces pasamos a tener

$\displaystyle \int_{\cosh(a)}^{\cosh(b)} \sqrt{x^2 - 1}dx = \int_{a}^{b} \sqrt{\cosh^{2} (u)- 1} \sinh du = \int_{a}^{b}  \sinh^{2} du$

Para resolver esta última integral debes proceder de forma similar a la integral de $\sin^{2}$ por partes.

Estoy dando solo a grandes pasos como realizarlo, pero si quieres verlo en profundidad vuelve a escribir

Repito que esta parte del ejercicio es sustancialmente mas dificil que el resto

Saludos