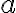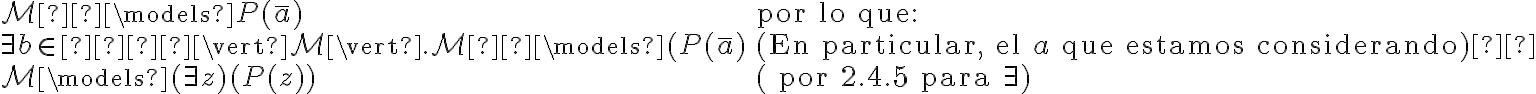Lógica: Cuantificadores

Buenas!, quería seria saber si el siguiente razonamiento es correcto. En una formula del estilo (∀z)(P(z)→((∃z)Q(z))) si quiero aplicar el 2.4.5 al hacer la sustitución del para todo en (P(z)→((∃z)Q(z))) quedaría (∀a∈M)(M⊨ P(a)→((∃z)Q(z)) (porque z en (∃z)Q(z) no esta libre por lo tanto no se hace la sustitución de a) . Luego nuevamente por el 2.4.5 del → se obtendría (∀a∈M)(M⊨ P(a)→ M⊨ ((∃z)Q(z))) y finalmente por el 2.4.5(y sustituyendo) quedaría (∀a∈M)(M⊨ P(a)→ (∃b∈M)(M⊨Q(b))). Desde ya muchas gracias!

Re: Cuantificadores

de Fernando Carpani - miércoles, 5 de junio de 2024, 16:01

Hola.
El rumbo no está mal... sólo que hay un problema en la escritura (usen latex !!!) para diferenciar qué es lenguaje y qué es metalenguaje.

Esto sería algo así (si no me comí nada...)

$\begin{array}{l l}\bar{\forall} a \in \vert \mathcal{M} \vert . \mathcal{M} \models (P(\bar{a}) \to (\exists z)(P(z)) & ( \text{ por 2.4.5 para } \forall ) \\\text{Por esto, tomando un } a \text{ arbitrario de } \vert \mathcal{M} \vert \text{se cumple que: } \\ \mathcal{M} \models (P(\bar{a}) \to (\exists z)(P(z))) \\ \mathcal{M} \models P(\bar{a}) \Rightarrow \mathcal{M} \models (\exists z)(P(z)) & \text{Por 2.4.5 para } \to \\\end{array}$

Para probar esta afirmación (el "meta-implica" anterior), suponemos ahora que efectivamente, tenemos un

$a$ arbitrario tal que (*):

$\begin{array}{l l}\mathcal{M} \models P(\bar{a}) & \text{por lo que:}\\\exists b \in \vert \mathcal{M} \vert . \mathcal{M} \models (P(\bar{a}) & (\text{En particular, el } a \text{ que estamos considerando}) \\\mathcal{M} \models (\exists z )(P(z)) & (\text{ por 2.4.5 para } \exists )\end{array}$

Espero que aclare.