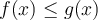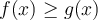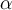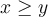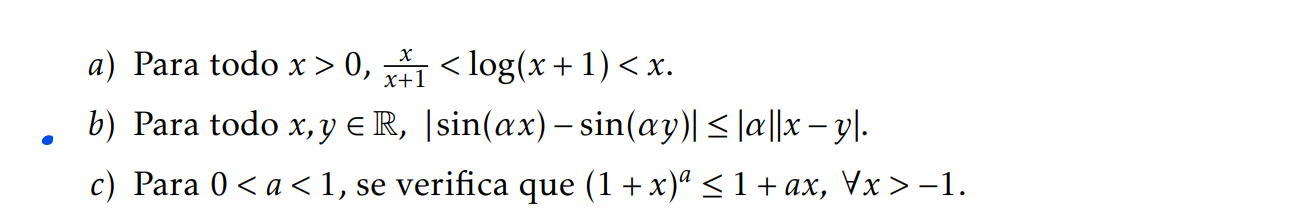
Buenas,
Sobre el ejercicio 10 parte b) de la seccion 6 monotonia,extremos y geometria me pide demostrar eso.
Mi idea es que si pruebo que la desigualdad se cumple para las derivadas pruebo la desigualdad. Lo que hice fue derivar a ambos lados pero no supe como seguir luego de eso. Me podrian dar una guia de como seguir?
saludos,