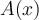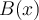Me pregunto por la unicidad de la inversa. De la lectura del material no se desprende directamente. Pero se llega a determinar su coeficiente enésimo. Pero este está determinado de forma recursiva, en función de los anteriores. Por lo que me entra la duda. Quizá exceda o no sea relevante para el curso. Pero me surgió la cuestión y quería plantearla.
Re: Inversa de una función generatriz
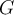 es el conjunto de funciones generatrices,
es el conjunto de funciones generatrices,  es invertible, y
es invertible, y  es el neutro del producto en
es el neutro del producto en 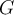 ; es decir,
; es decir,  .
. .
. en la expresión de la derecha, se llega a que
en la expresión de la derecha, se llega a que  .
. Re: Inversa de una función generatriz
Gracias
Re: Inversa de una función generatriz
Hola Roberto, es interesante tu pregunta y realmente se me pasó colocar un pequeño comentario sobre eso cuando escribí las notas.
La demostración de Miguel Ángel es correcta (esencialmente es la demostración que se ve en Teoría de Grupos para probar la unicidad del inverso en general).
En el caso particular de funciones generatrices es bastante más simple, solo basta notar que la sucesión (bn) (del principio de la página 8 de las notas) queda unívocamente determinada pues cada término b_n queda determinado conociendo todos los términos anteriores (hay que asumir que la sucesión (an) es dada). Y además (se desprende de la prueba que) la sucesión (bn) es la única que verifica las condiciones 1 y 2, que es equivalente a la invertibilidad.
Saludos,
Claudio.