GAL2-1S: Operador autoadjunto en DIM INFINITA

Buenas, en Openfing el profesor hizo un ejemplo en el cual el siguiente operador no tiene valores propios
$V = C ( [a,b] , \mathbb{C} ) = \{ f:[a,b] \rightarrow \mathbb{C} , \text{f continua} \}$ en $\mathbb{K} = \mathbb{C}$ y con el producto interno:

$\langle f,g \rangle = \displaystyle \int_{a}^{b} f(x) \overline{g(x)} dx$ $\forall f,g \in V$ Mi duda es la siguiente:

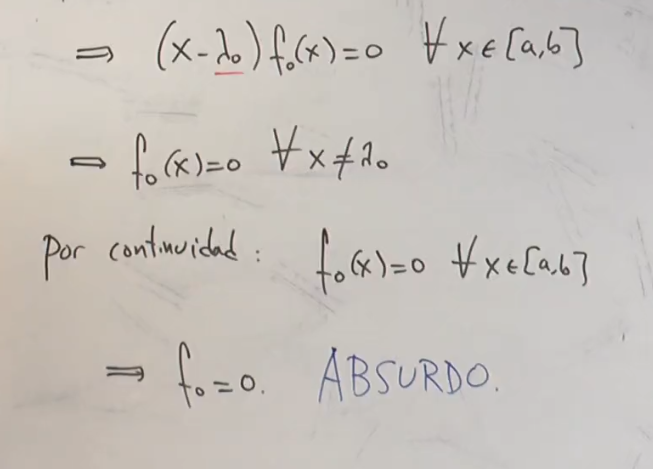
¿Qué aporta la continuidad en este caso? ¿Qué me determina eso que $f_0 (x) = 0 \Rightarrow f_0 = 0$ ?

Re: Operador autoadjunto en DIM INFINITA

de Juan Piccini - viernes, 31 de mayo de 2024, 18:49

Hola Alexis, como el EV es el espacio de las funciones continuas, si $\lambda_0\notin [a,b]$ entonces es claro que debe ser $f_0(x)=0\forall x\in [a,b]$ , y como las funciones constantes son continuas, debería ser $f_0=O_V$ y tienes el absurdo.

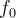Pero si $\lambda_0\in [a,b]$ , entonces perfectamente podría suceder que $f_0(x)=0\;\forall x\in [a,b],x\neq\lambda_0$ , $f_0(\lambda_0)=\lambda_0$ y se cumpliría la igualdad, pero esta $f_0$ no es un vector perteneciente al espacio porque no es continua (a menos que $\lambda_0=0$ ), no podríamos llegar a un absurdo.

La continuidad es la que te permite llegar al absurdo cuando $\lambda_0\in [a,b]$ .

Saludos.