Buenas noches, tengo una duda sobre este ejercicio:

Llegué a la siguiente igualdad (luego de haber hallado polinomio característico y sus raíces, junto a los subespacios asociados a cada 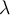 )
)
 siendo
siendo  , utilicé lo siguiente (cambio de base):
, utilicé lo siguiente (cambio de base):  con
con 
Entonces :  y a simple vista (y sabiendo que
y a simple vista (y sabiendo que  ) me queda que
) me queda que 
¿Es así el procedimiento o tengo que hacer algo más?
