Buenas
El problema se puede resolver de varias manera. Voy a usar una herramienta que se aplica para varios problemas.
Trabajaremos primero en el intervalo ![[0,\frac{1}{2}] [0,\frac{1}{2}]](https://eva.fing.edu.uy/filter/tex/pix.php/6f5d1434932730c96a74db6c217a5e86.png) . Supongamos por absurdo que
. Supongamos por absurdo que  para todo
para todo ![x \in (0,\frac{1}{2}] x \in (0,\frac{1}{2}]](https://eva.fing.edu.uy/filter/tex/pix.php/3045aaf3679cae144bafa0b2a6baae8e.png) .
.
Usaremos la propiedad que dice: sean  dos funciones derivables, si
dos funciones derivables, si  y
y  para todo
para todo  entonces
entonces 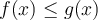 para todo
para todo  . Puedes ver esta propiedad para este caso en el ejercicio 6.7-8. En este caso concreto
. Puedes ver esta propiedad para este caso en el ejercicio 6.7-8. En este caso concreto  constante, puedes verlo aqui
constante, puedes verlo aqui
Esta propiedad puedes deducirla aplicando la relación entre crecimiento y derivada a la función  y es una herramienta que te resultara útil en el ejercicio 6.8-8.
y es una herramienta que te resultara útil en el ejercicio 6.8-8.
Pensemos ahora una función  cuya derivada segunda sea constante
cuya derivada segunda sea constante 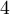 y
y 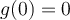 ,
,  . Podemos tomar por ejemplo
. Podemos tomar por ejemplo 
Como  y
y  tenemos entonces que
tenemos entonces que  para todo
para todo  .
.
Volviendo a aplicar la propiedad tenemos que  para todo
para todo  .
.
Ahora hay que observar que si  para algún
para algún 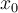 entonces
entonces  para todo
para todo ![x \in (x_{0},\frac{1}{2}] x \in (x_{0},\frac{1}{2}]](https://eva.fing.edu.uy/filter/tex/pix.php/0ce670a2e849362e2618f86dc2b9c348.png) y luego
y luego  para todo
para todo ![x \in (x_{0},\frac{1}{2}] x \in (x_{0},\frac{1}{2}]](https://eva.fing.edu.uy/filter/tex/pix.php/0ce670a2e849362e2618f86dc2b9c348.png) , en particular
, en particular  .
.
Si planteas el problema análogo en el intervalo  , con
, con  obtendrás que
obtendrás que  o bien
o bien 
Aquí obtuvimos dos opciones, o bien una formula explicita para  (en los intervalos
(en los intervalos ![(0,\frac{1}{2}] (0,\frac{1}{2}]](https://eva.fing.edu.uy/filter/tex/pix.php/9915d06b2bcd9324f58678de1336fc78.png) y
y  ) pero esta función no es dos veces derivable o bien una contradicción en
) pero esta función no es dos veces derivable o bien una contradicción en 
Cualquier cosa volve a preguntar
Saludos

