Buenas noches, hay algo que no me queda claro sobre cómo planteó Jazmín el ejercicio:
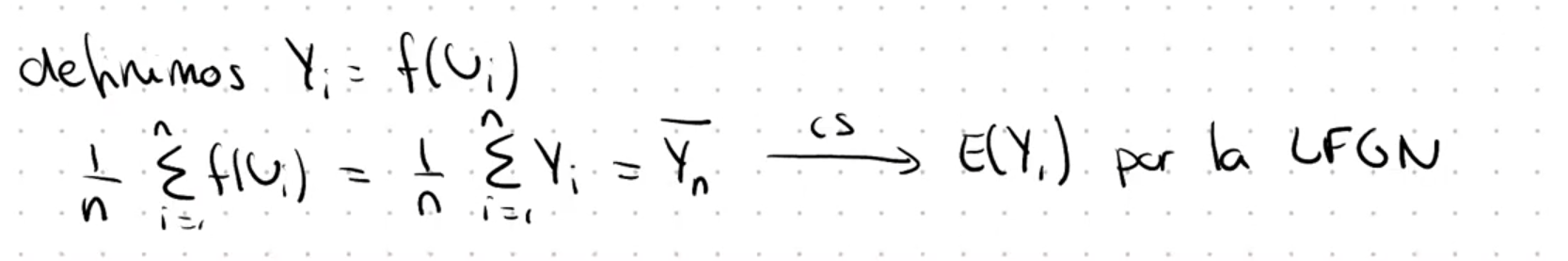
Se definió una nueva variable $$Y_i = f(U_i)$$ y luego trató de averiguar cuál es $$\mathbb{E} (Y_1)$$
De donde obtuvo lo siguiente:
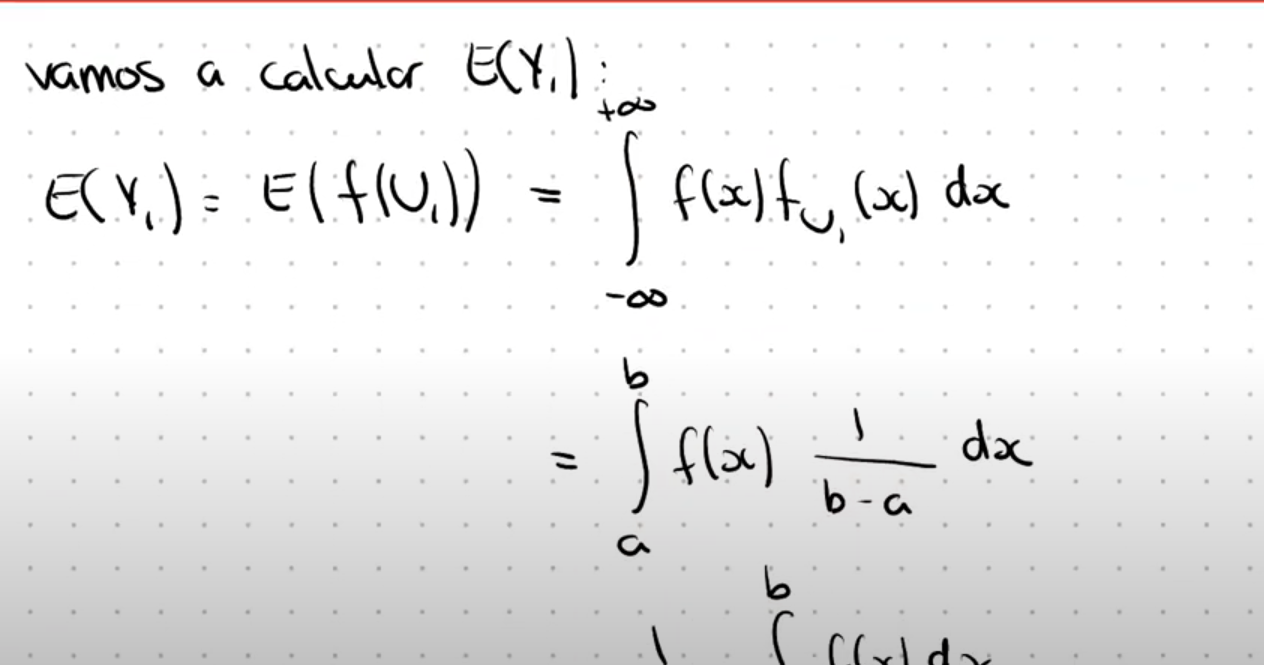
No comprendo $$\mathbb{E} (f(U_1)) = \displaystyle \int_{-\infty}^{+\infty} f(x) f_{U_1}(x) dx$$ , ¿ese $$f_{U_1}(x)$$ dentro de la integral es simplemente por definición de esperanza ( $$\mathbb{E} (x) = \displaystyle \int_{-\infty}^{+\infty} x f_X (x) dx$$ ) ? Porque luego considera lo que vale $$f_{U_i}(x) = \left\{ \begin{array}{lr} \frac{1}{b-a} & \text{si } x \in [a,b] \\ 0 & \text{si no} \end{array} \right.$$ y pasa a $$\displaystyle \int_{a}^{b} f(x) \frac{1}{b-a} dx $$
