Hola, Antonela
Con respecto al ejercicio 6, no entiendo bien tu pregunta. Al ser un movimiento plano, el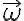 es perpendicular al dibujo, por lo que
es perpendicular al dibujo, por lo que 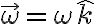 , y sólo deberías hallar
, y sólo deberías hallar  a través de aplicar distribución de velocidades entre dos puntos de velocidad conocida (A y B). Si esto no responde tu pregunta, mandame más específicamente que es lo que no te cierra.
a través de aplicar distribución de velocidades entre dos puntos de velocidad conocida (A y B). Si esto no responde tu pregunta, mandame más específicamente que es lo que no te cierra.
Con respecto al 11, tenés un error a la hora de calcular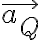 . El error que veo leyendo rápidamente es que está mal derivado
. El error que veo leyendo rápidamente es que está mal derivado 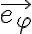 , dado que no usaste el
, dado que no usaste el 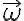 del versor (que es simplemente
del versor (que es simplemente 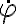 según
según 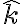 ), sino el del rígido.
), sino el del rígido.
Con respecto al ejercicio 6, no entiendo bien tu pregunta. Al ser un movimiento plano, el
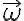 es perpendicular al dibujo, por lo que
es perpendicular al dibujo, por lo que 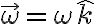 , y sólo deberías hallar
, y sólo deberías hallar  a través de aplicar distribución de velocidades entre dos puntos de velocidad conocida (A y B). Si esto no responde tu pregunta, mandame más específicamente que es lo que no te cierra.
a través de aplicar distribución de velocidades entre dos puntos de velocidad conocida (A y B). Si esto no responde tu pregunta, mandame más específicamente que es lo que no te cierra.Con respecto al 11, tenés un error a la hora de calcular
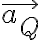 . El error que veo leyendo rápidamente es que está mal derivado
. El error que veo leyendo rápidamente es que está mal derivado 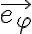 , dado que no usaste el
, dado que no usaste el 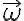 del versor (que es simplemente
del versor (que es simplemente 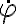 según
según 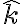 ), sino el del rígido.
), sino el del rígido.