Buenas
Veamos primero el caso donde  , luego trata de adaptar los argumentos al caso general y si tienes dudas vuelve a escribir.
, luego trata de adaptar los argumentos al caso general y si tienes dudas vuelve a escribir.
Tomemos un  con
con  . El caso
. El caso  es análogo y el caso
es análogo y el caso  se puede estudiar aparte.
se puede estudiar aparte.
Para encontrar la recta tangente debemos dar la circunferencia como una función de una variable y calcular la tangente a partir de la derivada, como estamos trabajando en este capítulo.
En este caso, la ecuación de la circunferencia es  . Por lo que para la semicircunferencia superior tenemos
. Por lo que para la semicircunferencia superior tenemos  .
.
El punto  pertenece a la semicircunferencia superior, es decir
pertenece a la semicircunferencia superior, es decir  y la recta tangente a la circunferencia por
y la recta tangente a la circunferencia por 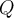 es
es
Por otro lado la recta que pasa por  es
es
En conclusión
Como  las rectas son perpendiculares
las rectas son perpendiculares
Agrego un pequeño bosquejo de la situación (con 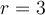 ), si continuas con dudas vuelve a escribir
), si continuas con dudas vuelve a escribir