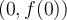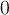Sea f : R → R una función derivable en 0, y r : R → R la ecuación de la recta tangente
por 0. Probar que r es la mejor aproximación lineal a f en 0, eso es, dada otra ecuación
lineal q : R → R existe un entorno de 0, el cual notamos I0
, donde para todo x ∈ I0 se
tiene que |f (x) − r(x)| ≤ |f (x) − q(x)|. Probar que además la igualdad se da solo en 0.
Esta es la letra del ejercicio. Ya probé la primera tesis, pero la segunda me confunde. f(0)-r(0) siempre es 0 (sino no sería recta tangente), pero que |f (x) − r(x)| = |f (x) − q(x)| si x = 0 implica que f(x) - q(x) = 0, es decir, implica que q también es recta tangente. O me equivoco?