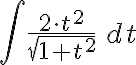Letra:
Sea C la curva dada por la intersección de las superficies:
con
orientada de modo que el punto inicial sea (1,0,0). Sea el campo F(x,y,z) = (y, -x, 1). Pide hallar la circulación del campo F sobre C.
Yo plantee:
de la segunda ecuación saqué que 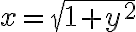
Entonces dije que la curva C es:
Porque en la cuva gamma, en 0 vale (1,0,0) y el otro término lo saqué igualando x de gamma a lo que dice la letra.
Después usé la definición para hallar la circulación y me quedó que tenía que integrar esto:
Obviamente hay algo mal pero no se que es, está bien en hallar la curva de esa manera?
Espero respuesta, gracias y saludos!
Edit: en la coordenada z de gamma, me faltó multiplicar por un t, pero las cuentas que le siguen estan bien.

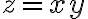
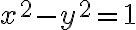
![x \epsilon \left[1, \frac{e+e^{-\left(1\right)}}{2} \right] x \epsilon \left[1, \frac{e+e^{-\left(1\right)}}{2} \right]](https://eva.fing.edu.uy/filter/tex/pix.php/2a2d9fa702ac7171eab8b95d58ac9f92.gif)
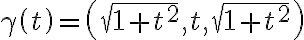
![t \epsilon \left[0, \frac{ \sqrt{e^{2}+e^{-\left(2\right)}-2} }{2} \right] t \epsilon \left[0, \frac{ \sqrt{e^{2}+e^{-\left(2\right)}-2} }{2} \right]](https://eva.fing.edu.uy/filter/tex/pix.php/b65bca7645edaae4ea9dbffa87857436.gif)