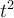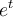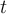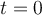Ejercicio 11

Ejercicio 11

de Gean Lucas Minetti Fernandez -
Número de respuestas: 3
Hola, este ejercicio logré hacerlo pero me surgió una duda.
Si en vez de pedir hallar los valores que mejor aproximan una recta o una parabola, se pidiera hallar los valores que mejor aproximan otra función cualquiera, como sería? Por ejemplo si la función es  y =  αe^x + βcos(x)
En respuesta a Gean Lucas Minetti Fernandez

Re: Ejercicio 11

de Luciano Matias Muñiz Manasliski -
Hola, Gean Lucas.
Bueno, sería muy parecido al anterior. En lugar de tener t^2 tenés e^t y en lugar de t , \cos(t).
Por ejemplo, si t=0 la primer ecuación ecuación queda 0=\alpha e^0+\beta\cos(0)=\alpha +\beta.
Haces lo mismo con todos los valores
¿Se entiende así?
Luciano
En respuesta a Gean Lucas Minetti Fernandez

Re: Ejercicio 11

de Juan Piccini -

Hola Gean.

En el caso que planteas tu familia de funciones sería \phi=\{\varphi_1,\varphi_2\} donde \varphi_1(t)=e^t,\;\varphi_2(t)=cos(t) , entonces la matriz quedaría de 2 x 4, la primera columna  se forma con los valores \varphi_1(t),\;t=0,1,3,4 , la segunda columna se forma con \varphi_2(t), \;t=0,1,3,4 . El resto sigue igual.

Resuelves el sistema (A^t.A).X=A^t.B y encuentras la pareja X=(\alpha,\beta) con la que obtienes la mejor función del tipo que planteas.

Saludos

J.