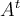Hola.
Tratando de resolver el ejercicio me planteé lo siguiente: trasponer la matriz de autos y combustibles que nos dan, ortonormalizar las columnas, proyectar el vector de combustibles sobre el subespacio de columnas, resolver el sistema Mv=P(u) donde M es la matriz de columnas ortonormalizadas, v es el vector de autos y P(u) es la proyección ortogonal del vector de combustibles sobre el subespacio de las columnas de M.
La cuestión es que me puse manos a la obra y me quedó y disparate de fracciones y raíces cuadradas, amén de la cantidad de cálculos que hubo que hacer. Intuyo que estoy cometiendo un error en alguna parte; serían tan amables de indicarme qué estaría haciendo mal?
Desde ya, muchas gracias.