Teorema Representación de Riesz (Existencia)

Teorema Representación de Riesz (Existencia)

de Alexis Sokorov Vargas -
Número de respuestas: 1

Buenas, tengo una duda respecto a lo siguiente:


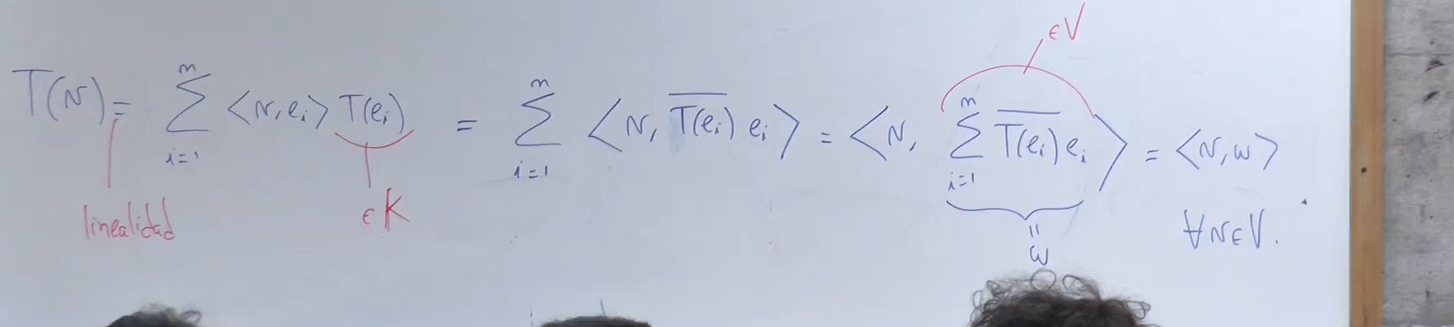
¿Cuál es la razón de que  \displaystyle T(v) =  \sum\nolimits_{i=1}^{n} \langle v , e_i \rangle T(e_i) = \sum\nolimits_{i=1}^{n} \langle v , \overline{T(e_i)} e_i \rangle ? ¿Qué aporta pasar para "adentro" del P.I. a T(e_i) ?
En respuesta a Alexis Sokorov Vargas

Re: Teorema Representación de Riesz (Existencia)

de Juan Piccini -

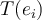Hola Alexis, el motivo está en la última igualdad: al juntar la suma de productos de v contra los vectores \overline{T}(e_i)e_i en un solo producto de v contra la suma de dichos vectores (que es un vector al que llaman w),  estás probando que T(v) puede expresarse como <v,w>, donde w es precisamente el vector que se obtiene como CL de la base ortonormal \{e_1,\dots,e_n\} , con coeficientes \overline{T}(e_1,\dots,\overline{T}(e_n)) .

Saludos

J.