Hola Rodrigo.
Si el sistema incompatible es , donde A es la matriz 4 x 3 que dices, entonces la solución aproximada es el X que resuelve el sistema
, donde A es la matriz 4 x 3 que dices, entonces la solución aproximada es el X que resuelve el sistema
Si el sistema incompatible es
 , donde A es la matriz 4 x 3 que dices, entonces la solución aproximada es el X que resuelve el sistema
, donde A es la matriz 4 x 3 que dices, entonces la solución aproximada es el X que resuelve el sistemaLo que haces es cambiar el término independiente B por su proyección sobre el subespacio generado por las columnas de A, llamémosle B'.
Como B-B' debe ser ortogonal a las columnas de A, (o sea a todas las filas de 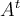 ), debe cumplirse que
), debe cumplirse que  , y como
, y como  (porque el sistema A.X=B' es compatible), sustituyendo se llega a que X (que es lo que llamamos solución aproximada) debe ser la solución del sistema
(porque el sistema A.X=B' es compatible), sustituyendo se llega a que X (que es lo que llamamos solución aproximada) debe ser la solución del sistema  .
.
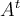 ), debe cumplirse que
), debe cumplirse que  , y como
, y como  (porque el sistema A.X=B' es compatible), sustituyendo se llega a que X (que es lo que llamamos solución aproximada) debe ser la solución del sistema
(porque el sistema A.X=B' es compatible), sustituyendo se llega a que X (que es lo que llamamos solución aproximada) debe ser la solución del sistema  .
.Saludos
J.