Hola Alexis, buenos días.
No logro entender el por qué de hallar el tiempo. La letra te pide la máxima posición transversal para un punto evaluado en x=0.25 m. Por ende, como sabés que el coseno (en valor absoluto) es menor o igual que 1, puedes imponer esta condición y sustituir x por la coordenada dada. Entiendo que parte de esto es lo que hiciste en tu razonamiento, pero no logro entender por qué dices que no te estaría dando "para ese x y t hallado"
Saludos,
m


 entonces traté de hallarlo cuando
entonces traté de hallarlo cuando 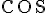 se hace máximo:
se hace máximo: