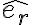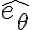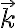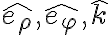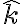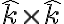Foro: parciales y exámenes

Buenas tardes estoy teniendo problemas en el cálculo de la aceleración absoluta de la partícula 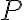$P$.

En primera instancia tengo estos resultados intermedios para el cálculo de la aceleración absoluta: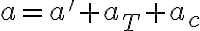

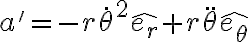
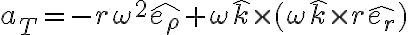
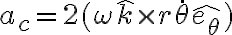
$a={a}'+a_{T}+a_{c}$
${a}'=-r\dot{\theta}^{2}\hat{e_{r}}+r\ddot{\theta}\hat{e_{\theta}}$
$a_{T}=-r\omega^{2}\hat{e_{\rho}}+\omega\hat{k}\times(\omega\hat{k}\times r\hat{e_{r}})$
$a_{c}=2(\omega\hat{k}\times r\dot{\theta}\hat{e_{\theta}})$

Se me complica visualizar geometrica y analiticamente los productos vectoriales: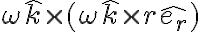
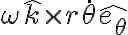$\omega\hat{k}\times(\omega\hat{k}\times r\hat{e_{r}})$ y $\omega\hat{k}\times r\dot{\theta}\hat{e_{\theta}}$, más que nada porque los versores tienen movimiento relativo entre ellos y no me doy cuenta exactamente porque en la solución del examen al realizar el producto vectorial quedan multiplicados por 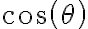$cos(\theta)$ y $sin(\theta)$

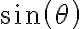
Si me pueden dar una mano para poder visualizar el porqué de esto les agradezco.

Aquí la solución de esta parte del examen.