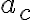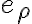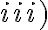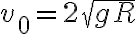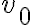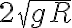Foro Práctico II

Buenas noches, no comprendo en qué me cambia tener una barra rígida en vez de una cuerda.
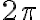
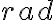La diferencia que veo es que mientras $\phi\in[\frac{-\pi}{2},\frac{\pi}{2}]$ la barra ejercerá una fuerza de tensión (tal como el hilo), mientras que si $\phi\in(\frac{\pi}{2},\frac{3\pi}{2})$, la barra ejercerá una fuerza Normal y por lo tanto podría continuar un movimiento circular completando $2\pi$ $rad$ (que creo no sería uniforme, pero sí se volvería una especie de bucle infinito dado que no hay disipación de energía).

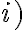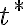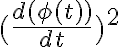En la parte $i)$, planteo que para un tiempo $t^*$ se tiene que $\frac{d(\phi(t))}{dt}(t^*)=0$ y de la ecuación de $(\frac{d(\phi(t))}{dt})^2$ encuentro que 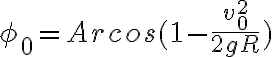$\phi_0=Arcos(1-\frac{v_0^2}{2gR})$. Pero al momento de analizar cuando se cumple que 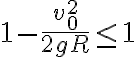$1-\frac{v_0^2}{2gR}\leq1$, aplicando la condición de que 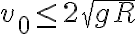$v_0\leq2\sqrt{gR}$ llego a que 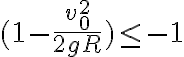$(1-\frac{v_0^2}{2gR})\leq-1$, lo cual significa en la igualdad que 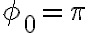$\phi_0=\pi$ (la partícula se detendría arriba del todo cual Kamikaze del Parque Rodó dejando a la gente de cabeza) y en la desigualdad que 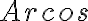$Arcos$ no estaría definido, contradiciendo lo que se me pide demostrar. Estoy un poco confundido, les agradezco si me pueden ayudar. Saludos.