Buen día Nicolás,
disculpa, pero no logro entender el razonamiento que hacés con los cambios de signo y cómo lo relacionás con la conservación.
Paso a corregirte un par de errores en el párrafo anterior y luego intentaré explicarlo de otra manera a ver si aclara las cosas.
Supongamos un sistema conservativo (que es el ejemplo que usaste), descrito por la siguiente ecuación de movimiento: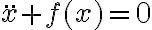 (hallada por Newton).
(hallada por Newton).
En primer lugar, creo que estás confundiendo la función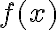 con la fuerza. No es exactamente la fuerza, de hecho, observá que no tiene las dimensiones correspondientes a dicha cantidad.
con la fuerza. No es exactamente la fuerza, de hecho, observá que no tiene las dimensiones correspondientes a dicha cantidad.
En segundo lugar, hay un error cuando decís "hago la derivada segunda de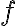 y evaluo los puntos de equilibrio en la derivada segunda". Si vas a trabajar con
y evaluo los puntos de equilibrio en la derivada segunda". Si vas a trabajar con 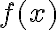 solo la derivás una vez para evaluar estabilidad. Aclaro esto porque tal vez aquí está ese cambio de signo que mencionás.
solo la derivás una vez para evaluar estabilidad. Aclaro esto porque tal vez aquí está ese cambio de signo que mencionás.
Ahora, pasemos a evaluar el mismo sistema a nivel energético. La ecuación de la energía tendrá una forma de este tipo:
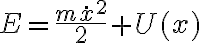
Derivando respecto al tiempo, obtenemos: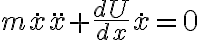 ,
,
esto es,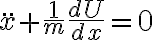 y, por tanto, en este caso,
y, por tanto, en este caso,  .
.
Allí podés observar que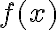 conserva el signo de
conserva el signo de 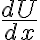 , entonces podés evaluar la estabilidad con la misma regla, derivando
, entonces podés evaluar la estabilidad con la misma regla, derivando 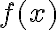 una vez respecto a
una vez respecto a 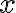 .
.
Espero haber respondido tu pregunta y se llegue a entender. Si no es así, lo mejor será que te acerques a una de las clases de consulta disponibles para discutirlo con más profundidad y que puedas evacuar todas tus dudas de forma más fluida.
Saludos.
disculpa, pero no logro entender el razonamiento que hacés con los cambios de signo y cómo lo relacionás con la conservación.
Paso a corregirte un par de errores en el párrafo anterior y luego intentaré explicarlo de otra manera a ver si aclara las cosas.
Supongamos un sistema conservativo (que es el ejemplo que usaste), descrito por la siguiente ecuación de movimiento:
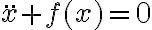 (hallada por Newton).
(hallada por Newton).En primer lugar, creo que estás confundiendo la función
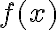 con la fuerza. No es exactamente la fuerza, de hecho, observá que no tiene las dimensiones correspondientes a dicha cantidad.
con la fuerza. No es exactamente la fuerza, de hecho, observá que no tiene las dimensiones correspondientes a dicha cantidad. En segundo lugar, hay un error cuando decís "hago la derivada segunda de
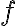 y evaluo los puntos de equilibrio en la derivada segunda". Si vas a trabajar con
y evaluo los puntos de equilibrio en la derivada segunda". Si vas a trabajar con 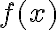 solo la derivás una vez para evaluar estabilidad. Aclaro esto porque tal vez aquí está ese cambio de signo que mencionás.
solo la derivás una vez para evaluar estabilidad. Aclaro esto porque tal vez aquí está ese cambio de signo que mencionás.Ahora, pasemos a evaluar el mismo sistema a nivel energético. La ecuación de la energía tendrá una forma de este tipo:
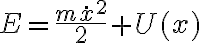
Derivando respecto al tiempo, obtenemos:
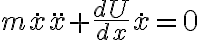 ,
,esto es,
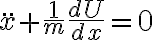 y, por tanto, en este caso,
y, por tanto, en este caso,  .
.Allí podés observar que
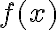 conserva el signo de
conserva el signo de 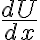 , entonces podés evaluar la estabilidad con la misma regla, derivando
, entonces podés evaluar la estabilidad con la misma regla, derivando 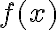 una vez respecto a
una vez respecto a 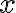 .
.Espero haber respondido tu pregunta y se llegue a entender. Si no es así, lo mejor será que te acerques a una de las clases de consulta disponibles para discutirlo con más profundidad y que puedas evacuar todas tus dudas de forma más fluida.
Saludos.
