buenas, queria consultar, como hago para distinguir en el caso de que pueda encontrar la preintegral por newton, independientemente de si se conserva o no la energia, tengo que pensarlo por medio del Ueff ahi para ver la estabilidad? y en el caso de que justo ese sistema conserve su energia, los puntos de equilibrio (con su respectivo equilibrio) evaluando por la conservacion de la energia deben de ser acordes a los encontrados por el Ueff no?
Duda Teorica. Potenial Efectivo y conservacion de la energia
Número de respuestas: 4
En respuesta a Nicolas Moreno Alsina
Re: Duda Teorica. Potenial Efectivo y conservacion de la energia
Hola Nicolás.
No es necesario evaluarlo siempre a nivel energético. El equilibrio y la estabilidad también pueden analizarse mediante la ecuación de movimiento calculada por la 2da. ley de Newton.
Cualquier sistema cuya ecuación de movimiento sea de la forma 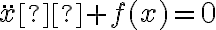 (siendo
(siendo  un grado de libertad) es preintegrable, sea o no conservativo.
un grado de libertad) es preintegrable, sea o no conservativo.
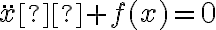 (siendo
(siendo  un grado de libertad) es preintegrable, sea o no conservativo.
un grado de libertad) es preintegrable, sea o no conservativo.La función 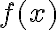 es proporcional (mediante una constante de proporcionalidad positiva) a la derivada respecto de x del potencial (o potencial efectivo, en caso de que corresponda). Es decir,
es proporcional (mediante una constante de proporcionalidad positiva) a la derivada respecto de x del potencial (o potencial efectivo, en caso de que corresponda). Es decir, 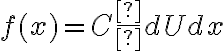 , con
, con 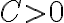 .
.
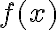 es proporcional (mediante una constante de proporcionalidad positiva) a la derivada respecto de x del potencial (o potencial efectivo, en caso de que corresponda). Es decir,
es proporcional (mediante una constante de proporcionalidad positiva) a la derivada respecto de x del potencial (o potencial efectivo, en caso de que corresponda). Es decir, 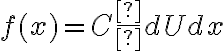 , con
, con 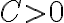 .
.La manera de evaluar el equilibrio es imponer 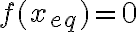 , lo que equivale a
, lo que equivale a 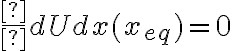 . Por otro lado, para evaluar la estabilidad, debemos evaluar el signo de
. Por otro lado, para evaluar la estabilidad, debemos evaluar el signo de 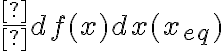 . Si esta es mayor que cero, el equilibrio es estable; si es menor, es inestable.
. Si esta es mayor que cero, el equilibrio es estable; si es menor, es inestable.
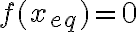 , lo que equivale a
, lo que equivale a 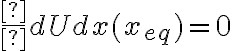 . Por otro lado, para evaluar la estabilidad, debemos evaluar el signo de
. Por otro lado, para evaluar la estabilidad, debemos evaluar el signo de 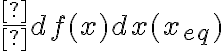 . Si esta es mayor que cero, el equilibrio es estable; si es menor, es inestable.
. Si esta es mayor que cero, el equilibrio es estable; si es menor, es inestable.Un último comentario; recordá que todo sistema conservativo es preintegrable (su ecuación de movimiento es el tipo 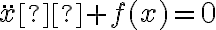 ). Los sistemas no conservativos pueden o no ser preintegrables.
). Los sistemas no conservativos pueden o no ser preintegrables.
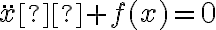 ). Los sistemas no conservativos pueden o no ser preintegrables.
). Los sistemas no conservativos pueden o no ser preintegrables.Saludos!
En respuesta a Florencia Benitez Martinez
Re: Duda Teorica. Potenial Efectivo y conservacion de la energia
genial, muchas graciass
En respuesta a Florencia Benitez Martinez
Re: Duda Teorica. Potenial Efectivo y conservacion de la energia
Buenas, me siguen quedando unas dudas, en el sentido de que si yo hallo la estabilidad de los puntos, mediante la conservacion de la energia, yo se que si la energia se conserva, entonces la fuerza deriva de menos un potencial energetico. entonces evaluando la segunda derivada de ese potencial, puedo sacar la estabilidad de los puntos de equilibrio evaluados, siendo mayor a cero estable, pero a la vez como decia arriba, si yo quiero relacionar esa derivada segunda de la energia con la fuerza, entonces la fuerza es menos ese potencial y se me invierten los signos. dejo una foto
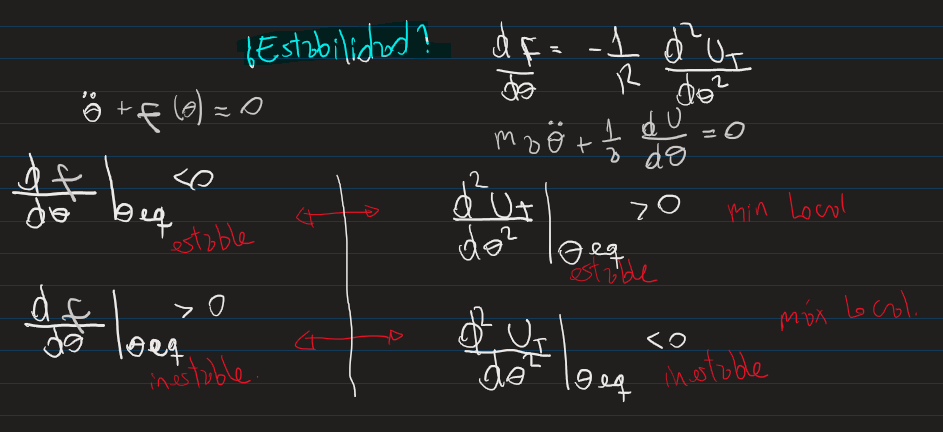
entonces eso me confunde un poco, en el sentido, de que si yo se que se conserva, hago la conservacion por energia, y me da tal cual la definicion de arriba, pero si yo no se si se conserva, yo aplico energia, y ahi me queda una funcion de la siguiente forma

y ahi operando, yo se que la estabilidad se da cuanto no hay aceleracion angular (el ejemplo de ese caso), entonces eso me condiciona que entonces ahí encuentro los theta de equilibrio, hago la derivada segunda de
entonces ahí encuentro los theta de equilibrio, hago la derivada segunda de  y evaluo los puntos de equilibrio en la derivada segunda y puedo obtener la estabilidad de los puntos evaluados, y aca normalmente, por las cosas de calculo y demas, yo se que si la funcion derivada 2 veces evaluada en el punto es mayor a cero, tiene un minimo, entonces posee un punto de estabilidad. pero ahora a lo que voy, si yo de un principio hice por newton, sin saber si se conservaba o no, me dio que eso de que para mayores que cero es estable, pero resulta que el sistema si se conserva , entonces me me esaria contradiciendo que para mayores que cero es inestable? porque cuando la energia se conserva ese ese - que me invierte los signos, pero si yo lo hago por newton directamente, ese signo de menos ya me queda implicito dentro de la f(thita) a la que llego?
y evaluo los puntos de equilibrio en la derivada segunda y puedo obtener la estabilidad de los puntos evaluados, y aca normalmente, por las cosas de calculo y demas, yo se que si la funcion derivada 2 veces evaluada en el punto es mayor a cero, tiene un minimo, entonces posee un punto de estabilidad. pero ahora a lo que voy, si yo de un principio hice por newton, sin saber si se conservaba o no, me dio que eso de que para mayores que cero es estable, pero resulta que el sistema si se conserva , entonces me me esaria contradiciendo que para mayores que cero es inestable? porque cuando la energia se conserva ese ese - que me invierte los signos, pero si yo lo hago por newton directamente, ese signo de menos ya me queda implicito dentro de la f(thita) a la que llego?
Para cerrar todo, si hago por newton, la derivada siempre tiene que ser > 0, para que sea estable independientemente si se conserva o no el sistema?

entonces eso me confunde un poco, en el sentido, de que si yo se que se conserva, hago la conservacion por energia, y me da tal cual la definicion de arriba, pero si yo no se si se conserva, yo aplico energia, y ahi me queda una funcion de la siguiente forma

y ahi operando, yo se que la estabilidad se da cuanto no hay aceleracion angular (el ejemplo de ese caso), entonces eso me condiciona que
 entonces ahí encuentro los theta de equilibrio, hago la derivada segunda de
entonces ahí encuentro los theta de equilibrio, hago la derivada segunda de 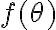 y evaluo los puntos de equilibrio en la derivada segunda y puedo obtener la estabilidad de los puntos evaluados, y aca normalmente, por las cosas de calculo y demas, yo se que si la funcion derivada 2 veces evaluada en el punto es mayor a cero, tiene un minimo, entonces posee un punto de estabilidad. pero ahora a lo que voy, si yo de un principio hice por newton, sin saber si se conservaba o no, me dio que eso de que para mayores que cero es estable, pero resulta que el sistema si se conserva , entonces me me esaria contradiciendo que para mayores que cero es inestable? porque cuando la energia se conserva ese ese - que me invierte los signos, pero si yo lo hago por newton directamente, ese signo de menos ya me queda implicito dentro de la f(thita) a la que llego?
y evaluo los puntos de equilibrio en la derivada segunda y puedo obtener la estabilidad de los puntos evaluados, y aca normalmente, por las cosas de calculo y demas, yo se que si la funcion derivada 2 veces evaluada en el punto es mayor a cero, tiene un minimo, entonces posee un punto de estabilidad. pero ahora a lo que voy, si yo de un principio hice por newton, sin saber si se conservaba o no, me dio que eso de que para mayores que cero es estable, pero resulta que el sistema si se conserva , entonces me me esaria contradiciendo que para mayores que cero es inestable? porque cuando la energia se conserva ese ese - que me invierte los signos, pero si yo lo hago por newton directamente, ese signo de menos ya me queda implicito dentro de la f(thita) a la que llego?Para cerrar todo, si hago por newton, la derivada siempre tiene que ser > 0, para que sea estable independientemente si se conserva o no el sistema?
En respuesta a Nicolas Moreno Alsina
Re: Duda Teorica. Potenial Efectivo y conservacion de la energia
Buen día Nicolás,
disculpa, pero no logro entender el razonamiento que hacés con los cambios de signo y cómo lo relacionás con la conservación.
Paso a corregirte un par de errores en el párrafo anterior y luego intentaré explicarlo de otra manera a ver si aclara las cosas.
Supongamos un sistema conservativo (que es el ejemplo que usaste), descrito por la siguiente ecuación de movimiento: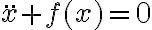 (hallada por Newton).
(hallada por Newton).
En primer lugar, creo que estás confundiendo la función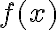 con la fuerza. No es exactamente la fuerza, de hecho, observá que no tiene las dimensiones correspondientes a dicha cantidad.
con la fuerza. No es exactamente la fuerza, de hecho, observá que no tiene las dimensiones correspondientes a dicha cantidad.
En segundo lugar, hay un error cuando decís "hago la derivada segunda de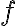 y evaluo los puntos de equilibrio en la derivada segunda". Si vas a trabajar con
y evaluo los puntos de equilibrio en la derivada segunda". Si vas a trabajar con 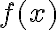 solo la derivás una vez para evaluar estabilidad. Aclaro esto porque tal vez aquí está ese cambio de signo que mencionás.
solo la derivás una vez para evaluar estabilidad. Aclaro esto porque tal vez aquí está ese cambio de signo que mencionás.
Ahora, pasemos a evaluar el mismo sistema a nivel energético. La ecuación de la energía tendrá una forma de este tipo:
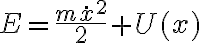
Derivando respecto al tiempo, obtenemos: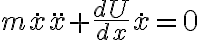 ,
,
esto es,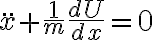 y, por tanto, en este caso,
y, por tanto, en este caso,  .
.
Allí podés observar que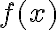 conserva el signo de
conserva el signo de 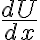 , entonces podés evaluar la estabilidad con la misma regla, derivando
, entonces podés evaluar la estabilidad con la misma regla, derivando 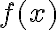 una vez respecto a
una vez respecto a 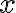 .
.
Espero haber respondido tu pregunta y se llegue a entender. Si no es así, lo mejor será que te acerques a una de las clases de consulta disponibles para discutirlo con más profundidad y que puedas evacuar todas tus dudas de forma más fluida.
Saludos.
disculpa, pero no logro entender el razonamiento que hacés con los cambios de signo y cómo lo relacionás con la conservación.
Paso a corregirte un par de errores en el párrafo anterior y luego intentaré explicarlo de otra manera a ver si aclara las cosas.
Supongamos un sistema conservativo (que es el ejemplo que usaste), descrito por la siguiente ecuación de movimiento:
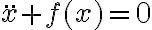 (hallada por Newton).
(hallada por Newton).En primer lugar, creo que estás confundiendo la función
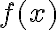 con la fuerza. No es exactamente la fuerza, de hecho, observá que no tiene las dimensiones correspondientes a dicha cantidad.
con la fuerza. No es exactamente la fuerza, de hecho, observá que no tiene las dimensiones correspondientes a dicha cantidad. En segundo lugar, hay un error cuando decís "hago la derivada segunda de
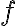 y evaluo los puntos de equilibrio en la derivada segunda". Si vas a trabajar con
y evaluo los puntos de equilibrio en la derivada segunda". Si vas a trabajar con 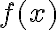 solo la derivás una vez para evaluar estabilidad. Aclaro esto porque tal vez aquí está ese cambio de signo que mencionás.
solo la derivás una vez para evaluar estabilidad. Aclaro esto porque tal vez aquí está ese cambio de signo que mencionás.Ahora, pasemos a evaluar el mismo sistema a nivel energético. La ecuación de la energía tendrá una forma de este tipo:
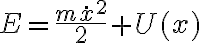
Derivando respecto al tiempo, obtenemos:
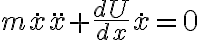 ,
,esto es,
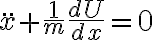 y, por tanto, en este caso,
y, por tanto, en este caso,  .
.Allí podés observar que
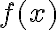 conserva el signo de
conserva el signo de 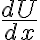 , entonces podés evaluar la estabilidad con la misma regla, derivando
, entonces podés evaluar la estabilidad con la misma regla, derivando 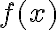 una vez respecto a
una vez respecto a 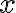 .
.Espero haber respondido tu pregunta y se llegue a entender. Si no es así, lo mejor será que te acerques a una de las clases de consulta disponibles para discutirlo con más profundidad y que puedas evacuar todas tus dudas de forma más fluida.
Saludos.
