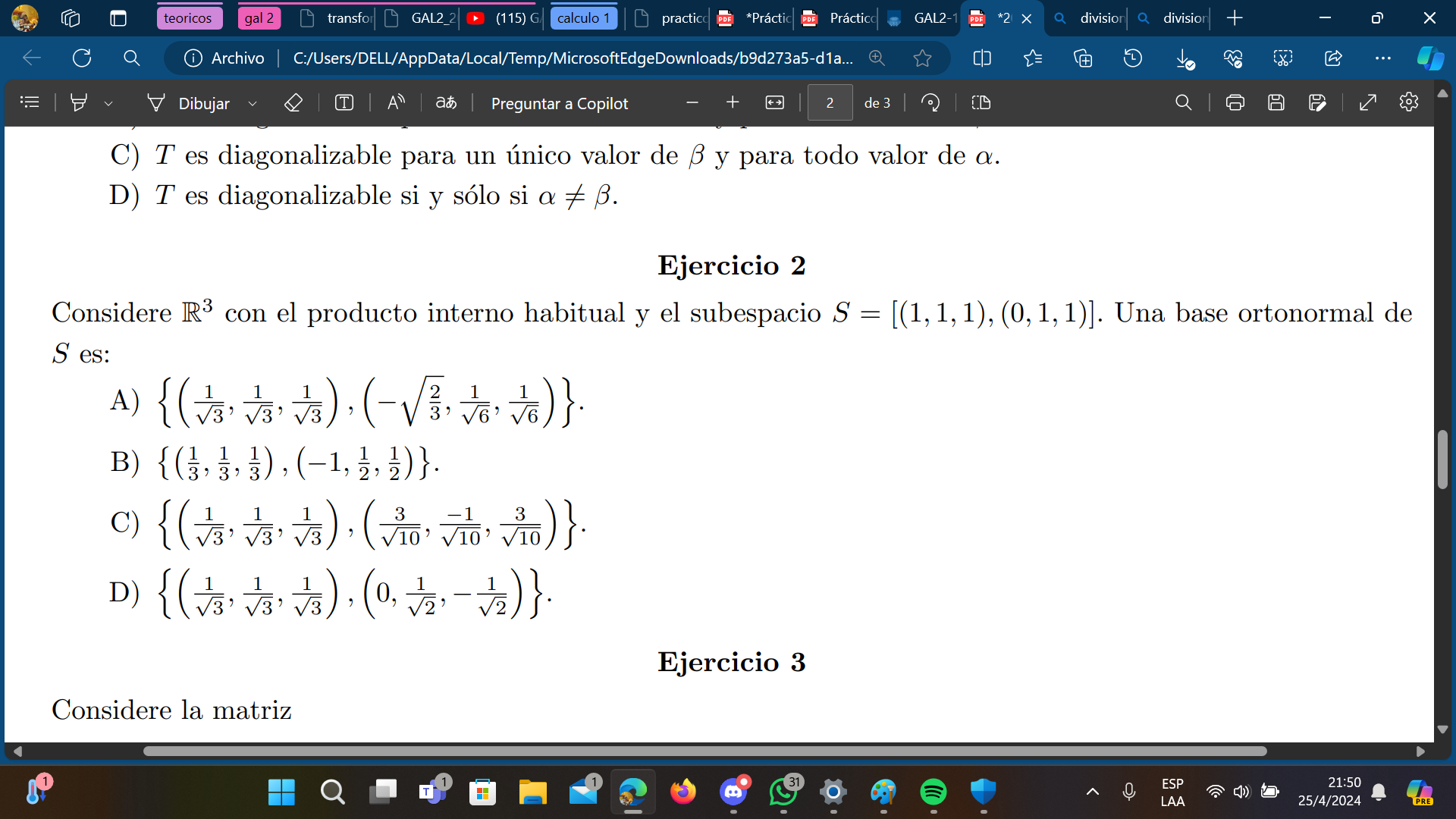
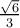la norma de w2 me da de (2^(1/2))/18
En respuesta a Andrés Guerri Cervantes
Re: no llego al final completo
Hola.
No sé qué es w2. Supongo que el vector que obtenés aplicando Gram-Schmidt. Digamos que es la base que se obtiene con ese método.
la base que se obtiene con ese método.
Es claro que por cuáles son las opciones (sin normalizar aún), la norma es
por cuáles son las opciones (sin normalizar aún), la norma es  .
.
Para obtener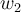 con Gram-Schmidt se le resta al otro vector la proyección ortogonal sobre el subespacio generado por
con Gram-Schmidt se le resta al otro vector la proyección ortogonal sobre el subespacio generado por 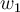 , es decir:
, es decir:

La norma de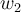 es
es  .
.
Luego
No sé qué es w2. Supongo que el vector que obtenés aplicando Gram-Schmidt. Digamos que es
 la base que se obtiene con ese método.
la base que se obtiene con ese método. Es claro que
 por cuáles son las opciones (sin normalizar aún), la norma es
por cuáles son las opciones (sin normalizar aún), la norma es  .
. Para obtener
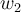 con Gram-Schmidt se le resta al otro vector la proyección ortogonal sobre el subespacio generado por
con Gram-Schmidt se le resta al otro vector la proyección ortogonal sobre el subespacio generado por 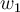 , es decir:
, es decir:
La norma de
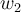 es
es  .
.Luego

En respuesta a Luciano Matias Muñiz Manasliski
Re: no llego al final completo
hola buenos días una consulta porque la norma de w2 termina quedando como 3 dividida raíz cuadrada de 6. Gracias
En respuesta a Agustina Mia Reyes Milán