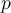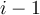Práctico 3 - Ejercicio 9

Práctico 3 - Ejercicio 9

de Nicolas Aguilera Leal -
Número de respuestas: 2

Buen día!

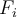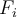De la letra del ejercicio no me queda claro cuál es el código que se está usando. Entiendo que al símbolo i se le asigna la palabra de código F_i. No me queda claro: Cuál es el tamaño del alfabeto? La letra dice que la palabra de código para i es el número F_i "redondeado a 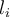l_i bits". Entonces 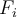F_i se representa en binario? Si es así, en qué representación? Punto flotante? Supongo que no porque sería muy complicado... Pero no entiendo el código. 

Gracias
En respuesta a Nicolas Aguilera Leal

Re: Práctico 3 - Ejercicio 9

de Maximo Pirri -
Buenas,
No entiendo de qué alfabeto hablas. La variable aleatoria toma valores entre 1 y m y se quiere construir un código para el caso en que X puede tomar 4 valores distintos. Fi se toma en binario si, donde por ejemplo 0.75 (que es F3) es 0.110000... pues es 0.5 (2 a la -1) + 0.25 (2 a la -2). Para determinar cuantos bits de esos se usan para una palabra de código hay que calcular la función techo del inverso de la probabilidad. Siguiendo el ejemplo de x3 se tiene que el logaritmo en base 2 de 1/0.125 es 3, por lo que se deben tomar los 3 bits más significativos después de la coma. Entonces x3 se codifica como 110.

Saludos.
En respuesta a Maximo Pirri

Re: Práctico 3 - Ejercicio 9

de Nicolas Aguilera Leal -
Entiendo la representación de F_i. Ahora me queda otra duda.

Si la distribución p fuese tal que p_i = 2^{-k} \forall i \in 1..m, F_i sería \sum_{k=1}^{i-1} 2^{-k} = 0.111...1 con i-1 bits en 1. Luego F_{i+1} = F_i + 2^{-i} = 0,1111...11 con i bits en 1. Entonces F_{i+1} sería prefijo de F_i y no se cumple lo que dice la letra que tengo que mostrar. Creo que esa distribución cumple con las condiciones que pone la letra. 

Seguro me estoy equivocando en algo, pero no veo dónde.