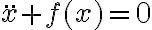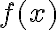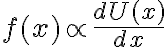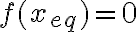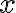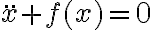Buenas, quería consultar sobre estos apuntes de una clase de práctico. En la parte c).
Nosotros dimos que para hallar los puntos de estabilidad/inestabilidad necesitamos la derivada segunda de la energía respecto a la posición, pero en este caso toma el termino de la ecuación de movimiento (con la aceleración igualada a cero) y lo deriva respecto a la posición, y ahí sustituye los puntos de equilibrio para ver si son estables o no.
Quería saber porque esta forma de resolver la estabilidad de los puntos de equilibrio es posible.