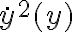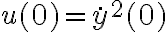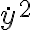Hola, Lucía
Cuando llegas a tu ecuación de movimiento, tenés dos opciones para resolverla.
- Caso 1: considerar el cambio de variable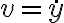 y resolver
y resolver 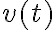 haciendo variables separables (u otro método) en la ecuación que te queda (que es de primer orden no lineal).
haciendo variables separables (u otro método) en la ecuación que te queda (que es de primer orden no lineal).
- Caso 2: considerar el cambio de variable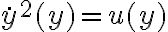 . Una vez que hagas este cambio de variable, llegás a una ecuación lineal de primer orden donde la variable independiente pasa a ser "y" y no "t". Es un camino que elimina la variable tiempo.
. Una vez que hagas este cambio de variable, llegás a una ecuación lineal de primer orden donde la variable independiente pasa a ser "y" y no "t". Es un camino que elimina la variable tiempo.
El camino que encares va a depender de lo que quieras saber. En este ejercicio se piden las dos cosas (partes i y ii). Tu encaraste solamente el caso 2, pero tenés mal la variable independiente en la solución que encontraste.
Cuando llegas a tu ecuación de movimiento, tenés dos opciones para resolverla.
- Caso 1: considerar el cambio de variable
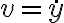 y resolver
y resolver 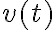 haciendo variables separables (u otro método) en la ecuación que te queda (que es de primer orden no lineal).
haciendo variables separables (u otro método) en la ecuación que te queda (que es de primer orden no lineal).- Caso 2: considerar el cambio de variable
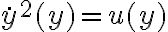 . Una vez que hagas este cambio de variable, llegás a una ecuación lineal de primer orden donde la variable independiente pasa a ser "y" y no "t". Es un camino que elimina la variable tiempo.
. Una vez que hagas este cambio de variable, llegás a una ecuación lineal de primer orden donde la variable independiente pasa a ser "y" y no "t". Es un camino que elimina la variable tiempo.El camino que encares va a depender de lo que quieras saber. En este ejercicio se piden las dos cosas (partes i y ii). Tu encaraste solamente el caso 2, pero tenés mal la variable independiente en la solución que encontraste.