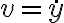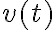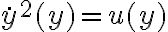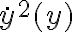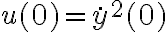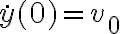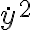MecNew: Ejercicio 4

Buenas tardes, en este ejercicio mi enfoque fue separar el caso en el que la bala sube del caso en el que baja por el signo de la fuerza de arrastre, planteé Newton y para resolver la ecuación diferencial intenté el cambio de variable sugerido en el curso de openfing. Con ese cambio de variable me queda una ecuación diferencial de primer orden con coeficientes constantes pero cuando la resuelvo no sé como revertir el cambio de variable ni como imponerle las condiciones iniciales. Necesitaría ayuda para identificar el error, y si simplemente es incorrecto el procedimiento me gustaría saber de que forma encararlo. Muchas gracias.

ej 4 mn p1

ej 4 mn p2

Re: Ejercicio 4

de Agustin Laguarda - martes, 16 de abril de 2024, 14:53

Hola, Lucía
Cuando llegas a tu ecuación de movimiento, tenés dos opciones para resolverla.
- Caso 1: considerar el cambio de variable

$v= \dot{y}$ y resolver

$v(t)$ haciendo variables separables (u otro método) en la ecuación que te queda (que es de primer orden no lineal).
- Caso 2: considerar el cambio de variable

$\dot{y}^2(y) = u(y)$ . Una vez que hagas este cambio de variable, llegás a una ecuación lineal de primer orden donde la variable independiente pasa a ser "y" y no "t". Es un camino que elimina la variable tiempo.
El camino que encares va a depender de lo que quieras saber. En este ejercicio se piden las dos cosas (partes i y ii). Tu encaraste solamente el caso 2, pero tenés mal la variable independiente en la solución que encontraste.

Cuando lo corrijas, vas a llegar a

$\dot{y}^2(y)$ . para eso vas a tenér que relacionar

$u(0) = \dot{y}^2(0)$ con las condiciones iniciales, que en este caso es

$\dot{y}(0)=v_0$ .

Luego, para ver a qué altura se detiene, simplemente tenés que igualar la expresión de

$\dot{y}^2$ a cero.

Cualquier cosa repreguntá.
Saludos!