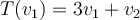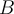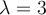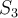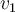Ejercicio 9.2

Ejercicio 9.2

de Pablo Daniel Falero Estevez -
Número de respuestas: 4

Luego de hallar la base del Subespacio asociado a 3 me quedan dos vectores, el (0,1,1)y el (1,0,0) , para hallar el tercer vector de la base de Jordan , hago T-3I igual a cualquier vector de la base y me queda sistema incompatible, me gustaria saber donde me equivoque o la solución 

En respuesta a Pablo Daniel Falero Estevez

Re: Ejercicio 9.2

de Martin Schmidt Agorio -
Hola Pablo,
Efectivamente: una base del subespacio propio asociado al 3 es {(1,0,0), (0,1,1)}. Ahora bien, lo que te dice jordan es que existe una base B = {w1,w2,w3} tal que _{B}(T)_{B} = \begin{bmatrix} 3 & 0 & 0\\ 0 & 3 & 0\\0 & 1 & 3 \end{bmatrix}
Entonces, se debe cumplir:
T(w1) = 3*w1 (1)
T(w2) = 3*w2 + w3 (2)
T(w3) = 3*w3 (3)

w3 debe ser vector propio asociado al 3 y además debe ser tal que existe un w2 que verifique (2). Pero el sistema (T-3I) (w2) = w3 no tiene solución para cualquier vector propio (como tu bien decis). Habría que escoger un vector propio que además haga que ese sistema sea compatible. Una forma es tomarse un w3 generico : w3 = (a,b,b) y ver que relacion deben tener a y b para que el sistema sea compatible. De los posibles w3 escoges uno y luego resolvés el sistema para hallar w2. 

Una vez que tengas w2 y w3 , para w1 tomás otro vector propio cualquiera que sea LI con w3 .
En respuesta a Martin Schmidt Agorio

Re: Ejercicio 9.2

de Alexis Sokorov Vargas -
Buenas! Llegué a lo siguiente en este ejercicio:
_B(T)_B = \begin{pmatrix}3&0&0\\1&3&0\\0&0&3\end{pmatrix} , y tengo que hallar una base B= \begin{Bmatrix}v_1 , v_2 , v_3\end{Bmatrix} tal que se cumpla lo siguiente
T(v_1)=3v_1 + v_2
T(v_2)=3v_2
T(v_3)=3v_3

De donde saco: (T - 3Id)(v_1)=v_2 ; (T-3Id)(v_2)=0 ; (T-3Id)(v_3)=0 en la ecuación del medio podría reescribirla como (T-3Id)^2(v_1)=0 pero no sé si sea correcto hacer eso.
Luego no sé cómo proseguir ni como hallar los vectores de la base B que mencioné
También sé que v_2 , v_3 son vep's asociados a \lambda = 3 entonces podría elegir a esos vectores como los que forman a S_3 supongo, de donde v_2 =(1,0,0) y v_3=(0,1,1) pero a la hora de hallar v_1 me ocurre lo mismo que al compañero, me queda un S.C.Indet. , no sé cómo hallar de otra forma ese v_1 para que me complete la base B