Hola a todos,
Me queda claro que el problema "Set covering" busca el mínimo de zonas a elegir (M) con el que se cubran todas las especies, y que no es el objetivo del ejercicio hallar el mínimo M.
Ahora bien, si el objetivo es hallar la cantidad de formas distintas de elegir M zonas que incluyan todas las especies, voy a reducir el problema para mostrar las dificultades con las que me encontré.
Supongamos que M = 2 y esta es mi matriz P:
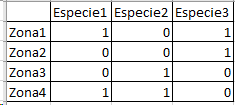
Si en cada replicación:
1. Elijo 2 zonas al azar
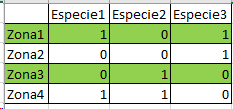
2. En esas 2 zonas evalúo si se representan todas las especies (Afirmativo para el ejemplo)
3. Si se incluyen todas las especies aumento un contador S (S=1 para el ejemplo)
4. Elimino las 2 zonas seleccionadas de mi matriz P
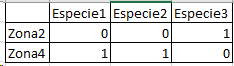
5. Elijo otras 2 zonas al azar (Hasta agotar las zonas)
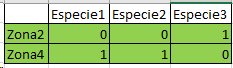
6. En esas 2 zonas evalúo si se representan todas las especies (Afirmativo para el ejemplo)
7. Si se incluyen todas las especies aumento un contador S (S=2 para el ejemplo)
8. Elimino las 2 zonas seleccionadas de mi matriz P (Ya no hay mas zonas)
Al hacer varias replicaciones (El ejemplo anterior vendría siendo la replicación #2):
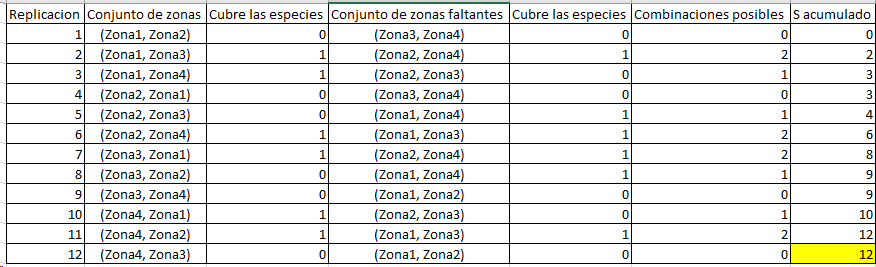
Analíticamente, para el ejercicio que planteo, la cantidad de combinaciones para el M=2, sería 2 (Zona1,Zona3 y Zona2,Zona4).
Mi conflicto es que S resulta con el mismo valor de la cantidad de replicaciones, es decir S/n = 1, y en el ejercicio 7.1 parte b, el valor de S me está dando mayor que n, y no sé cuál sería mi r (¿4 zonas?)
Si alguien tiene otro enfoque, les agradezco la ayuda.
Saludos.