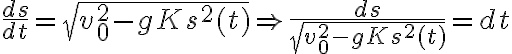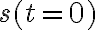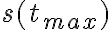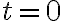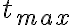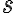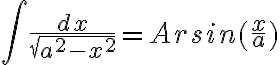Buenas tardes, no se estaría ocurriendo como hallar el tiempo que demora en detenerse. Ya hallé la velocidad pero no se de que condición saldría lo del tiempo. Necesitaría que me tirarán alguna ayuda. Desde ya muchas gracias.
Hola Lucía,
Si ya hallaste la velocidad en función del tiempo, la condición para que la partícula se detenga es que la velocidad se anule.
Lo siguiente es evaluar para qué tiempo se cumple esa condición.
Saludos.
Sigo sin saber bien como hallar el tiempo, estoy trancada con esta ecuación.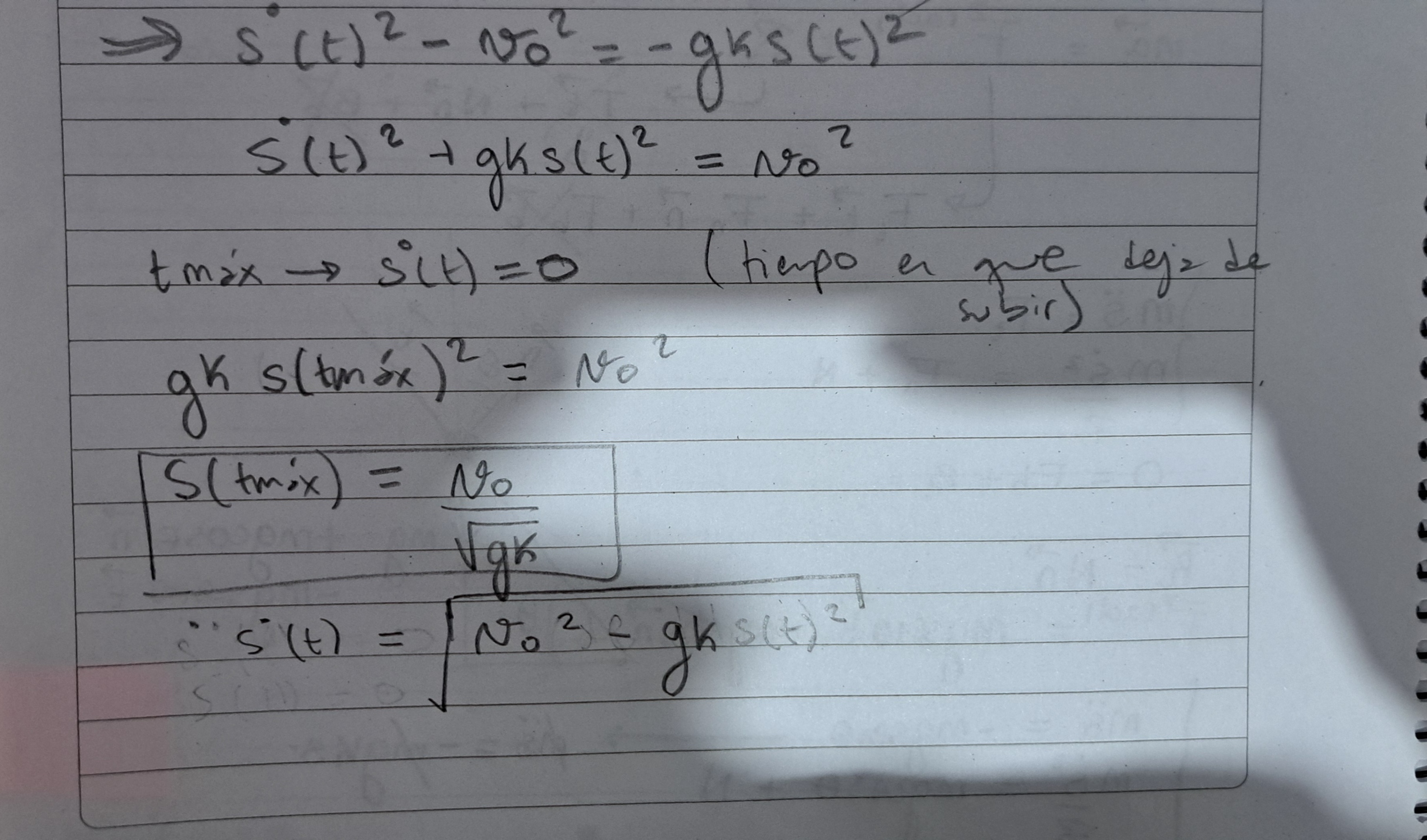
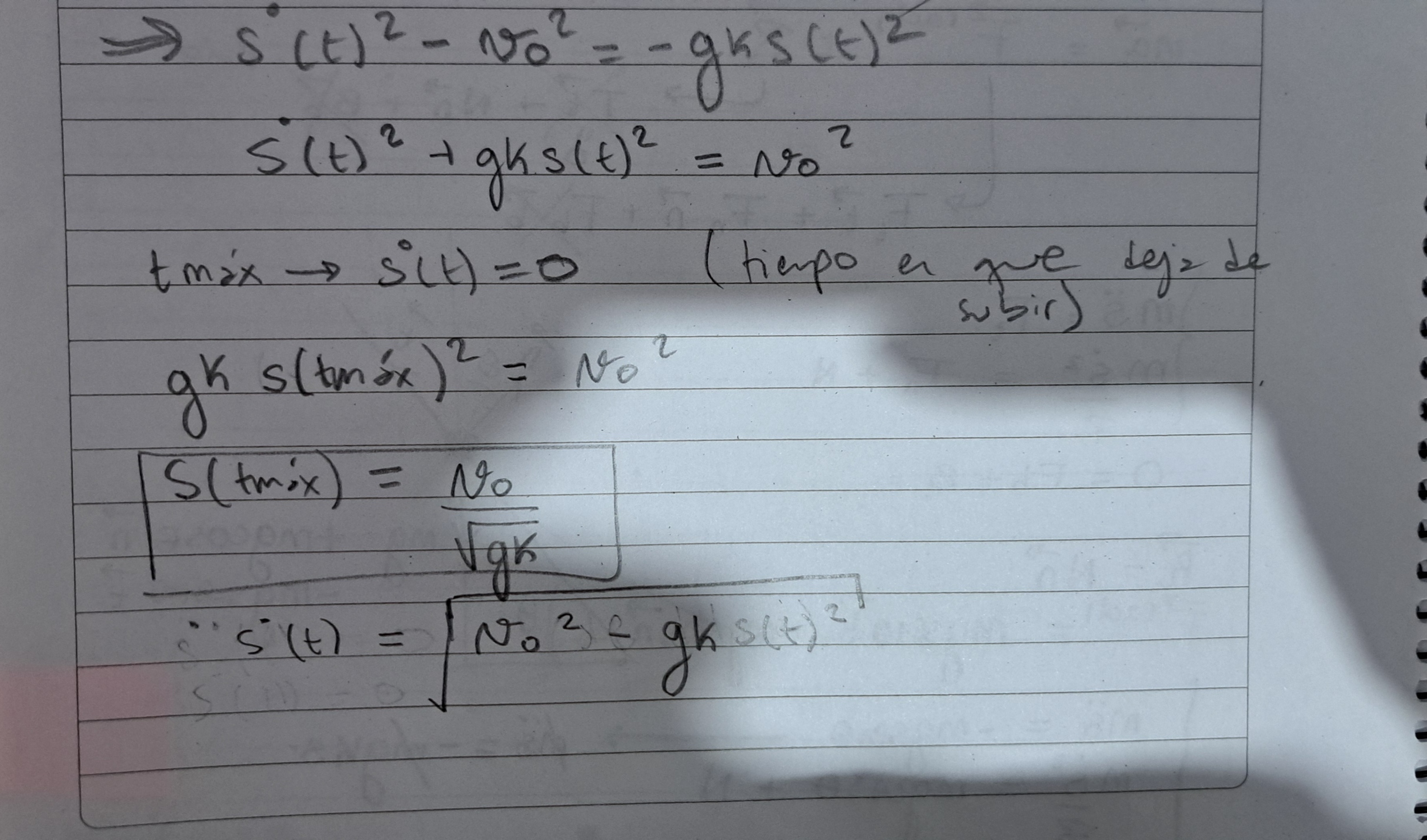
Buenas, yo lo que hice ahí es hacer variables separables. Si te fijas tenes 
. Y ahí directamente podes integrar de 
a 
, y de 
a 
. La integral de 
me costo darme cuenta, pero simplemente hay que tener en cuenta que 
. Así es como entiendo se puede hacer, saludos.
. Y ahí directamente podes integrar de a , y de a . La integral de me costo darme cuenta, pero simplemente hay que tener en cuenta que . Así es como entiendo se puede hacer, saludos.Lo voy a intentar, muchas gracias!