Hola.
SI, es correcto.
La forma de verlo es revisar la definición de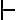 
(ver Pag 43 del pdf si no le erro):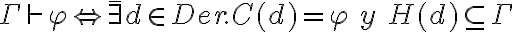
En esto,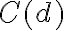 
es la conclusión de la derivación d y 
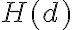son las hipótesis sin cancelar de la derivación.
Ese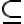 
hace que, en el caso que d no tenga hipótesis sin cancelar, d verifique todos los juicios 
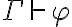sin importar el contenido de 
.
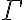Otro efecto de esa definición es el que construye la derivación no está obligado a usar todas las hipótesis; sólo usa las que necesita de acuerdo a las reglas que usa.