Sobre la definicion de teorema

Sobre la definicion de teorema

de Camilo Ferrero Alvarez -
Número de respuestas: 2

Hola buenas,

Antes que nada una peque;a disculpa por no tener tildes. Estaba viendo la definicion de teorema y segun entendi no debe tener hipotesis sin cancelar o goblales. Supongo que sale de la regla de introduccion del implica (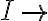I \rightarrow) y la cancelacion que trae consigo, la cual tiene justificacion en que si la premisa es falsa, puedo conculir cualquier cosa y sera cierto.

O sea si por ejemplo 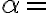 \alpha = "Tengo un triangulo rectangulo" y 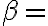\beta = Enunciado de Pitagoras, no necesito escribir 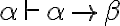\alpha \vdash \alpha \rightarrow \beta porque lo que no es triangulo rectangulo tambien cumple Pitagoras, no tengo cateto ni hipotenusa.

Pero en el caso de 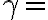\gamma = "Tengo una funcion continua y acotada" y 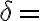\delta = "Es Riemann integrable" No seria necesario en este caso tener a 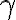\gamma como una hipotesis global? Porque lo que no es funcion continua y acotada no es Riemann integrable No dejaria entonces de ser un teorema bajo la definicion mencionada? O el error lo tengo yo cuando interpreto la negacion e intento "llevar a la semantica" esta deduccion?

Saludos y Gracias,
Camilo.
En respuesta a Camilo Ferrero Alvarez

Re: Sobre la definicion de teorema

de Fernando Carpani -
Hola.
A ver.... creo que entendí tu pregunta, si no es así, corregime.
El primer punto, es que yo tengo una hipótesis general, entonces puedo "eliminarla" CAMBIANDO mi juicio:

α⊢β⇒⊢α→βα⊢β⇒⊢α→β

Esto es aplicando la introducción de la implicación.

Por otro lado, si tengo una derivación que justifica ⊢α→β⊢α→β, puedo obtener
ββ tomando αα como hipótesis y aplicando eliminación del implica. O sea que se cumpliría también el juicio
α⊢βα⊢β .

Por esto, puedo afirmar que:
⊢α→β⇒α⊢β⊢α→β⇒α⊢β

Esto hace que:

⊢α→β⇔α⊢β⊢α→β⇔α⊢β

Y qué significa esto? Que si "llevamos a la semántica" (me gustó la frase :-)) las dos ideas ( \vdash , \to   ) son la misma, hablando en términos semánticos...

En los dos casos, tenemos la idea de consecuencia lógica, sólo que las expresiones (fórmulas de PROP) correctas \to están dentro del lenguaje, mientras que las que usan  \vdash   siempre están en el metalenguaje.

Como dije antes, espero haber entendido tu pregunta.
Saludos
FDO.