Foro de dudas de teórico

Hola Juan.

Tu hipótesis es que las matrices son semejantes y quieres probar que ambas matrices son matrices asociadas a un mismo operador T, sólo que en distintas  bases.

Lo primero es asociarle un operador a la matriz A, esto se hace como ya has visto.

Como $B=P^{-1}AP$, la matriz P tiene que ser una matriz de cambio de base, ya que sabemos de antes que dadas 2 matrices asociadas a un mismo operador, el cambio de base es lo que permite pasar de una matriz a otra.

De esto se deduce que P tiene que ser la matriz de cambio de base de una cierta base U a la canónica.

Como las coordenadas de un vector de 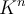$K^n$ en la base canónica de 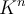$K^n$ coinciden con el vector, es claro que U tiene que estar formada por las columnas de P.

Las columna i-sima de P se obtiene haciendo el producto de P con el i-simo vector de la base canónica, por eso la base U se forma con los vectores $Pe_1,Pe_2,\dots,Pe_n$, que es otra forma de decir "las columnas de P".

Saludos

J..