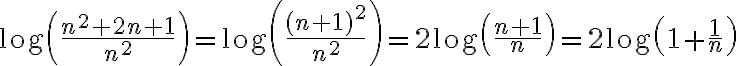Foro Práctico 4

Hola. Si el término general de la serie fuese equivalente a 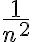$\displaystyle \frac{1}{n^2}$, entonces la serie debería ser convergente. Sin embargo, esta serie diverge. El problema de tu prueba está en la penúltima igualdad cuando calculás el límite: te faltó multiplicar por 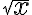$\sqrt{x}$ al 1 que está en el denominador, por lo que ese límite da 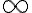$\infty$, así que el término general de la serie no es equivalente a $\displaystyle \frac{1}{n^2}$.

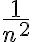Como sugerencia, podés tratar de probar que el término general de la serie es equivalente a 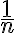$\displaystyle \frac{1}{n}$, cuya serie diverge. Una forma de ver eso sería observando que 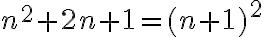$n^2+2n+1=(n+1)^2$, y por lo tanto:

$\displaystyle \log\left( \frac{n^2+2n+1}{n^2} \right) = \log\left( \frac{(n+1)^2}{n^2} \right) = 2 \log \left( \frac{n+1}{n} \right) = 2 \log \left( 1+\frac{1}{n} \right)$

También podés usar esa expresión para escribir la sucesión de sumas parciales y ver que tiende a infinito.

Saludos