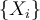Buen día. En el ejercicio 2 del práctico 2, si supongo que X0 -> X(n-1) -> Xn es una cadena de Markov, logro probar bastante rápido que H(X0 | Xn) >= H(X0 | X(n-1)), pero ¿por qué puedo suponer X0 -> X(n-1) -> Xn?
Saludos.
Hola, para ver que son de Markov yo plantee que cómo 
es de Markov 
, entonces 
y por definición estás tres variables forman una cadena de Markov.
Lo que yo no logré hacer es mostrar que H(X0 | Xn) >= H(X0 | X(n-1)) a pesar de que sé que es una cadena de Markov. Cómo hiciste eso?
es de Markov , entonces y por definición estás tres variables forman una cadena de Markov.Lo que yo no logré hacer es mostrar que H(X0 | Xn) >= H(X0 | X(n-1)) a pesar de que sé que es una cadena de Markov. Cómo hiciste eso?
Hola,
yo use la desigualdad de procesamiento de datos, si
entonces 
, después usas la definición de información y te queda esa expresión. Capaz estoy haciendo algo mal, no lo se.
Saludos.
yo use la desigualdad de procesamiento de datos, si
entonces , después usas la definición de información y te queda esa expresión. Capaz estoy haciendo algo mal, no lo se.Saludos.
Buenas,
La idea que plantea Ignacio es correcta y por ese camino se llega a la desigualdad.
Saludos.
La idea que plantea Ignacio es correcta y por ese camino se llega a la desigualdad.
Saludos.