Buenas tardes.
Les agradezco si puede darme alguna idea para resolver la parte c) de este ejercicio, porque no me estoy dando cuenta. Lo que observo es que las 
raíces de un número complejo constituyen los vértices de un polígono regular centrado en el origen, cosa que apliqué para la parte a). Por lo tanto, entiendo que los 
con 
segmentos son iguales, ya que es condición de un polígono regular; a lo que el productorio de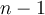 
lados de esos sería 
. He probado para 
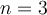y verifico que se cumple porque 
, por lo que cada segmento mide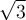 
y por lo tanto el productorio de 
lados es 
. No sabría como continuar.
Hola.
Lo que decís de que son todos iguales no es cierto para n>3. Para n=4 fijate que el primero y el último son lados del cuadrado pero el segundo es una diagonal.
La sugerencia a lo que apunta es lo siguiente: Si podemos calcular el producto de los (Q_i - Q_1) para i entre 2 y n, el producto de sus módulos es simplemente el módulo del producto. Observar que ese producto es exactamente x^n -1 si se factorizan todas las raíces (que por definición de Q_i son precisamente los Q_i) evaluado en 1, solo que sobra el factor de x-1 (que vendría a ser medir la distancia del 1 al 1). Por eso se te sugiere que factorices x^n-1 usando la fórmula de a^n - b^n y sigas desde ahí.
Saludos,
Gabriel
Lo que decís de que son todos iguales no es cierto para n>3. Para n=4 fijate que el primero y el último son lados del cuadrado pero el segundo es una diagonal.
La sugerencia a lo que apunta es lo siguiente: Si podemos calcular el producto de los (Q_i - Q_1) para i entre 2 y n, el producto de sus módulos es simplemente el módulo del producto. Observar que ese producto es exactamente x^n -1 si se factorizan todas las raíces (que por definición de Q_i son precisamente los Q_i) evaluado en 1, solo que sobra el factor de x-1 (que vendría a ser medir la distancia del 1 al 1). Por eso se te sugiere que factorices x^n-1 usando la fórmula de a^n - b^n y sigas desde ahí.
Saludos,
Gabriel
Hola Gabriel, entendí mejor el ejercicio luego de leer tu respuesta, pero no me doy cuenta de por qué el producto es exactamente 
. No veo esto: "Observar que ese producto es exactamente x^n -1 si se factorizan todas las raíces (que por definición de Q_i son precisamente los Q_i) evaluado en 1".
. No veo esto: "Observar que ese producto es exactamente x^n -1 si se factorizan todas las raíces (que por definición de Q_i son precisamente los Q_i) evaluado en 1".Si hago el productorio obtengo |
|. Desarrollé un poco varios de los productos pero no llego a nada que me llame la atención.
|. Desarrollé un poco varios de los productos pero no llego a nada que me llame la atención.