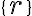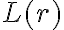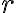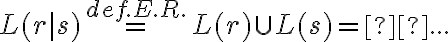Hola!
Estaba haciendo este ejercicio y algo de mi notación me hacía un poco de ruido. Lo encaré por definición de ER, es decir:
(r|s) = {r} U {s} = {r,s} = {s,r} = {s} U {r} = (s|r).
Ahora, lo que me hace ruido es escribir {r} como tal, ya que r es una expresión regular, y escribiendo eso estoy diciendo "el conjunto de la expresión regular r" lo cual no tiene mucho sentido a mi parecer.
Agradezco me dijeran si esa forma de demostrar está bien y sobretodo mi notación. (También pensé en encararlo por L(r|s) = L(s|r) y así no andar metiendo conjuntos raros que yo me invento como {r}).