Hola Diego. La respuesta corta es que sí, siempre se puede ya que todo ejercicio que sale por inducción común también sale por inducción fuerte, en este caso concreto es más simple usar inducción común con paso base
La principal forma de darte cuenta qué método usar en la práctica es intentar probar el paso inductivo (más abajo te doy más detalle que quiero decir con esto) y eso te va a decir que método es más conveniente y cuántos "casos bases" vas a precisar. Por supuesto, después de hacer muchos ejemplos, para muchos ejercicios ya te vas a dar cuenta con solo mirarlo si sale más simple con inducción fuerte o inducción común ya te alcanza.
A continuación te doy una respuesta más general con consejos prácticos de cuándo te conviene usar una u otra y cuántos casos bases precisás hacer al aplicar el principio de inducción fuerte (PIF).
En el caso concreto del ejercicio, la afirmación a demostrar sería
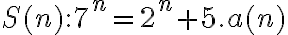
para algún natural a(n) que depende de n.
El ejercicio pide probar que S(n) es verdadera para todo
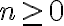
.
Para ver si se entiende, para n=0 tenés
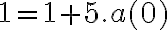
y entonces la afirmación es válida pues podés tomar a(0)=0.
Para n=1 tenés
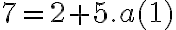
y entonces la afirmación es válida pues puedes tomar a(1)=1.
Para n=2 tenés
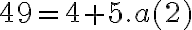
y entonces la afirmación es válida pues puedes tomar a(2)=9.
Y así sucesivamente, ¿cuándo parar? ¿cuántos casos bases serán necesario para el paso base? ¿sale por inducción común o voy a precisar inducción fuerte?
Consideramos entonces en general, que tenés un ejercicio que te pide probar que cierta afirmación S(n) es válida para todo natural
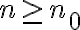
para algún natural
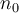
fijo (en el caso del ejercicio 6
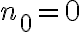
).
1. Al principio podés plantearte una inducción:
Paso base:
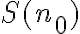
es verdadera (a través de un chequeo directo)
Hipótesis inductiva (H.I): Todas las afirmaciones
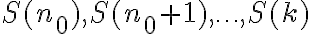
son ciertas para un cierto valor fijo de

.
Tesis inductiva (T.I):
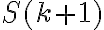
es cierta.
El paso inductivo consiste en probar que H.I implica T.I.
Si lograste probar eso sin asumir nada extra respecto de k entonces conseguiste probar el ejercicio y se terminó.
(obs. en el caso que solo fue necesario usar que S(k) es verdadera entonces podrías haber usado inducción común también)
Si para la demostración del paso inductivo no te alcanzó con suponer que
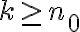
sino que precisaste usar que
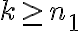
para cierto
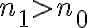
, entonces tenés que "reforzar" el caso base para que el argumento por inducción funcione, ya que tenés que agregar dentro del paso base la veracidad de la afirmación S(k) para todos los valores entre
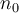
y
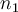
y el planteo correcto sería:
Paso base:
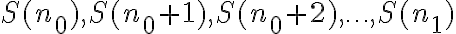
son verdaderas (chequear esto directamente)
Hipótesis inductiva: Todas las afirmaciones
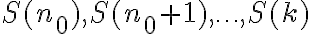
son ciertas para un cierto valor fijo de

.
Tesis inductiva:
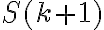
es cierta.
Entonces, la respuesta a tu pregunta de cuántos "casos bases" vas a precisar, depende del valor de
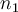
y ese valor solo te vas a dar cuenta una vez que intentes probar el paso inductivo (no hay una receta general).
Espero haberte aclarado pero cualquier cosa que no se entienda podés volver a preguntar.
Saludos,
Claudio
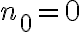
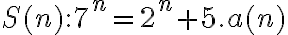 para algún natural a(n) que depende de n.
para algún natural a(n) que depende de n.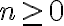 .
.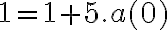 y entonces la afirmación es válida pues podés tomar a(0)=0.
y entonces la afirmación es válida pues podés tomar a(0)=0.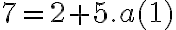 y entonces la afirmación es válida pues puedes tomar a(1)=1.
y entonces la afirmación es válida pues puedes tomar a(1)=1.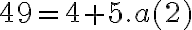 y entonces la afirmación es válida pues puedes tomar a(2)=9.
y entonces la afirmación es válida pues puedes tomar a(2)=9.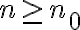 para algún natural
para algún natural 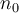 fijo (en el caso del ejercicio 6
fijo (en el caso del ejercicio 6 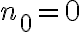 ).
).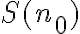 es verdadera (a través de un chequeo directo)
es verdadera (a través de un chequeo directo)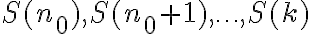 son ciertas para un cierto valor fijo de
son ciertas para un cierto valor fijo de  .
.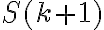 es cierta.
es cierta.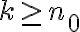 sino que precisaste usar que
sino que precisaste usar que 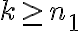 para cierto
para cierto 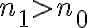 , entonces tenés que "reforzar" el caso base para que el argumento por inducción funcione, ya que tenés que agregar dentro del paso base la veracidad de la afirmación S(k) para todos los valores entre
, entonces tenés que "reforzar" el caso base para que el argumento por inducción funcione, ya que tenés que agregar dentro del paso base la veracidad de la afirmación S(k) para todos los valores entre 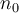 y
y 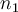 y el planteo correcto sería:
y el planteo correcto sería: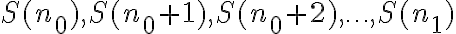 son verdaderas (chequear esto directamente)
son verdaderas (chequear esto directamente)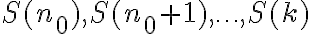 son ciertas para un cierto valor fijo de
son ciertas para un cierto valor fijo de  .
.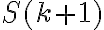 es cierta.
es cierta.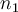 y ese valor solo te vas a dar cuenta una vez que intentes probar el paso inductivo (no hay una receta general).
y ese valor solo te vas a dar cuenta una vez que intentes probar el paso inductivo (no hay una receta general).