Práctico 1 - Foro de consultas

Buenas.

La parte (a) se puede hacer usando inducción. Para probar el paso inductivo podés hacer lo que te sugieren en otra respuesta, que consiste en escribir: 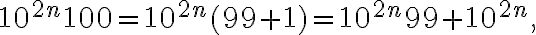$10^{2n} 100 = 10^{2n} (99 + 1) =10^{2n} 99 + 10^{2n} ,$ y usar la hipótesis de inducción.

La parte (b) ya la veo más difícil para hacer por inducción. Una alternativa a usar inducción, es usar el Teorema del binomio. Este teorema lo vieron en MD1, y es la siguiente identidad: 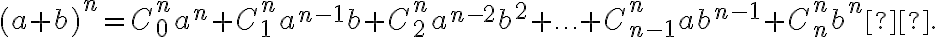$(a+b)^n = C^n_0 a^n+ C^n_1 a^{n-1} b + C^n_2 a^{n-2} b^2 + \ldots + C^n_{n-1} a b^{n-1} + C^n_n b^n  .$

En este ejercicio en particular, la idea es usar la identidad de la siguiente forma (para la parte (a) por ejemplo):

$10^{2n} = (10^2)^n = 100^n = (99+1)^n = 99^n+ C^n_1 99^{n-1} + C^n_2 99^{n-2} + \ldots + C^n_{n-1} 99 + 1 .$

Esto prueba que 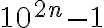$10^{2n} - 1$ es múltiplo de 99 (sin usar inducción). Por lo tanto: 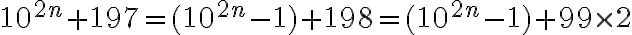$10^{2n} + 197 = ( 10^{2n} - 1 ) + 198 = ( 10^{2n} - 1 ) + 99 \times 2$, es múltiplo de 99.

En la parte (b) pueden usar este razonamiento para relacionar 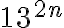$13^{2n}$. En este caso hay que hacer un paso más, haciendo aparecer el 56 antes de usar el binomio (o después sino).

Saludos.