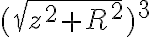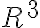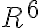Entiendo que es un caso de oscilador armónico simple, sin embargo no se como resolverlo, porque si trato de hallar lo equivalente a la constante elástica del caso del resorte me sigue dependiendo de la posición de la particula en el eje.
Verás, el problema es que la distancia (z) es "muy pequeña comparada al radio" (z<<<R), la parte que te sigue quedando en función de la distancia seguramente sea (sqrt(z²+R²))³, pero cuando z es muy pequeño, esa raíz tiende únicamente a R², que elevado al cubo queda R^6.
Así solamente te queda un z multiplicando de un lado de la igualdad y la aceleración del otro lado, así sacas la frecuencia.
Hola,
¡gracias Vicente por tu respuesta! Solo quisiera agregar un par de comentarios.
Joaquín, efectivamente, para resolver este ejercicio hay que llegar a una ecuación del tipo oscilador armónico simple: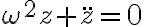
. Para obtener esta ecuación podés aplicar la segunda ley de Newton a la partícula, usando la aproximación 
<<
.
¡gracias Vicente por tu respuesta! Solo quisiera agregar un par de comentarios.
Joaquín, efectivamente, para resolver este ejercicio hay que llegar a una ecuación del tipo oscilador armónico simple:
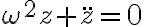. Para obtener esta ecuación podés aplicar la segunda ley de Newton a la partícula, usando la aproximación <<.En este caso, en la expresión del campo eléctrico hay involucrado un término del tipo
, que tiende a 
cuando es pequeño (cuidado, no tiende a 
).Saludos,
Nahuel