Buenas, en las notas del curso se llega a que el método de Heun es condicionalmente absolutamente estable y que h < 2/|lambda| (llamaré a lambda L por comodidad a partir de ahora). Pero al hacerlo por mi cuenta llego a: |1 + hL*(2 + hL)| < 1 (expresión equivalente a la que se llega en el libro) lo cual infiere que para que eso se cumpla: -1 < |hL*(2 + hL)| < 0. En el caso |hL*(2 + hL)| < 0 llego a lo mismo que las notas, pero en el caso de -1 < |hL*(2 + hL)| me queda una solución en los complejos a la cual solo puedo dar la región de estabilidad: Re = {|1 + z + (z^2)/2| < 1} siendo z = hL y perteneciente a los complejos.
La consulta es, por qué podría afirmar que h < 2/|L|? Hay algún análisis con los números complejos que me estoy perdiendo o alguna propiedad que me permite afirmar eso?
Desde ya, muchas gracias
En respuesta a Mateo Sebastian Gargano Alvarez Y Alvarez
Re: Estabilidad método de Heun
Hola Mateo,
Creo que no llegaste a la misma expresión que a la que llegamos en las notas. Con tu notación, en las notas queda |1+hL*(1+hL/2)|<1 (es la fórmula que está abajo de (6.34)). Tampoco me queda claro cómo de ahí llegás a la expresión -1 < |hL*(2 + hL)| < 0.
Creo que no llegaste a la misma expresión que a la que llegamos en las notas. Con tu notación, en las notas queda |1+hL*(1+hL/2)|<1 (es la fórmula que está abajo de (6.34)). Tampoco me queda claro cómo de ahí llegás a la expresión -1 < |hL*(2 + hL)| < 0.
En respuesta a Juan Pablo Borthagaray
Re: Estabilidad método de Heun
Perdón, tuve un error al escribir lo que me quedó en mi razonamiento, lo que me quedó fue: |1 + (hL/2)(2 + hL)| < 1. La razón por la cual luego llego a que -2 < (hL/2)(2 + hL) < 0 (cometí otro erro al poner -1 y no -2) es porque para que se cumpla una desigualdad de la forma |1 + x| < 1, se precisa que x sea negativo (porque sino 1 + x > 1) y que sea mayor a -2 (porque sino 1 + x < -1 => |1 + x| > 1). De igual forma, a pesar de los errores anteriores, al resolver la desigualdad -2 < (hL/2)(2 + hL) me sigue quedando una solución compleja. Le seguí dando vueltas al asunto y como justificación a que se cumple esta desigualdad es que haciendo cuentas -2 < (hL/2)(2 + hL) => (hL)^2 + 2hL + 4 > 0 y con un cambio de variabe x = hL queda resolver x^2 + 2x + 4 > 0. Con esto, puedo decir que geométricamente la funcion x^2 + 2x + 4 siempre es positiva para todo x en los reales. Esta sería una justificación valida?
En respuesta a Mateo Sebastian Gargano Alvarez Y Alvarez
Re: Estabilidad método de Heun
Bien, ahora creo que te estoy siguiendo mejor.
Tomamos como punto de partida que en el curso estamos trabajando con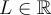 en el problema test. Si no, la conclusión
en el problema test. Si no, la conclusión  no sería correcta. La desigualdad
no sería correcta. La desigualdad  implica, como bien decís, que
implica, como bien decís, que  (estoy asumiendo desde el arranque que
(estoy asumiendo desde el arranque que 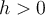 y
y  ).
).
Hay que interpretar bien lo que significa que la otra desigualdad no tenga soluciones reales. Lo que decís al final creo que va en la dirección correcta: la desigualdad se cumple para todos
no tenga soluciones reales. Lo que decís al final creo que va en la dirección correcta: la desigualdad se cumple para todos  (y en particular para
(y en particular para 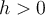 y
y  ). Eso quiere decir que esta desigualdad no agrega ninguna restricción sobre las que ya teníamos.
). Eso quiere decir que esta desigualdad no agrega ninguna restricción sobre las que ya teníamos.
[Como comentario al margen, si querés estudiar qué pasa con , entonces tendrías que entender la desigualdad
, entonces tendrías que entender la desigualdad  con módulo y ahí te quedaría una región en el plano complejo (podés encontrar un dibujo por ahí, en particular está al final de la sección 11.3 en el libro de Quarteroni-Sacco-Saleri). Esa región compleja es distinta que la que corresponde al método de Euler hacia adelante, pero su intersección con el eje real es igual; eso explica por qué en las notas del curso nos quedaron las mismas restricciones en el paso para Euler y para Heun.]
con módulo y ahí te quedaría una región en el plano complejo (podés encontrar un dibujo por ahí, en particular está al final de la sección 11.3 en el libro de Quarteroni-Sacco-Saleri). Esa región compleja es distinta que la que corresponde al método de Euler hacia adelante, pero su intersección con el eje real es igual; eso explica por qué en las notas del curso nos quedaron las mismas restricciones en el paso para Euler y para Heun.]
Tomamos como punto de partida que en el curso estamos trabajando con
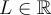 en el problema test. Si no, la conclusión
en el problema test. Si no, la conclusión  no sería correcta. La desigualdad
no sería correcta. La desigualdad  implica, como bien decís, que
implica, como bien decís, que  (estoy asumiendo desde el arranque que
(estoy asumiendo desde el arranque que 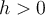 y
y  ).
). Hay que interpretar bien lo que significa que la otra desigualdad
 no tenga soluciones reales. Lo que decís al final creo que va en la dirección correcta: la desigualdad se cumple para todos
no tenga soluciones reales. Lo que decís al final creo que va en la dirección correcta: la desigualdad se cumple para todos  (y en particular para
(y en particular para 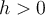 y
y  ). Eso quiere decir que esta desigualdad no agrega ninguna restricción sobre las que ya teníamos.
). Eso quiere decir que esta desigualdad no agrega ninguna restricción sobre las que ya teníamos.[Como comentario al margen, si querés estudiar qué pasa con
 , entonces tendrías que entender la desigualdad
, entonces tendrías que entender la desigualdad  con módulo y ahí te quedaría una región en el plano complejo (podés encontrar un dibujo por ahí, en particular está al final de la sección 11.3 en el libro de Quarteroni-Sacco-Saleri). Esa región compleja es distinta que la que corresponde al método de Euler hacia adelante, pero su intersección con el eje real es igual; eso explica por qué en las notas del curso nos quedaron las mismas restricciones en el paso para Euler y para Heun.]
con módulo y ahí te quedaría una región en el plano complejo (podés encontrar un dibujo por ahí, en particular está al final de la sección 11.3 en el libro de Quarteroni-Sacco-Saleri). Esa región compleja es distinta que la que corresponde al método de Euler hacia adelante, pero su intersección con el eje real es igual; eso explica por qué en las notas del curso nos quedaron las mismas restricciones en el paso para Euler y para Heun.]
En respuesta a Juan Pablo Borthagaray
Re: Estabilidad método de Heun
Muchas gracias por la respuesta y la bibliografia recomendada!