Hola Alexis,
Con el cambio a polares que hiciste (sin hacer el cambio de variables que es la traslación antes) te quedan otros límites de integración, no los que pusiste. La bola de centro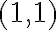 y radio
y radio  está determinada por la ecuación
está determinada por la ecuación 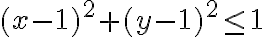 . Si sustituimos a
. Si sustituimos a  por
por 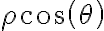 y a
y a  por
por  vemos que no nos quedan muy lindos los límites de integración.
vemos que no nos quedan muy lindos los límites de integración.
Lo que plantea la solución es escribir polares con centro en el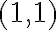 , por eso primero hace una traslación que lleva al
, por eso primero hace una traslación que lleva al 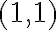 al origen, y lleva a la bola del domino a la bola centrada en el origen, y luego sí hace polares.
al origen, y lleva a la bola del domino a la bola centrada en el origen, y luego sí hace polares.
Espero ayude el comentario, cualquier cosa volvé a escribir nomás.
Saludos,
Leandro
Con el cambio a polares que hiciste (sin hacer el cambio de variables que es la traslación antes) te quedan otros límites de integración, no los que pusiste. La bola de centro
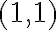 y radio
y radio  está determinada por la ecuación
está determinada por la ecuación 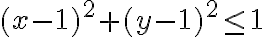 . Si sustituimos a
. Si sustituimos a  por
por 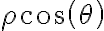 y a
y a  por
por  vemos que no nos quedan muy lindos los límites de integración.
vemos que no nos quedan muy lindos los límites de integración.Lo que plantea la solución es escribir polares con centro en el
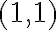 , por eso primero hace una traslación que lleva al
, por eso primero hace una traslación que lleva al 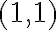 al origen, y lleva a la bola del domino a la bola centrada en el origen, y luego sí hace polares.
al origen, y lleva a la bola del domino a la bola centrada en el origen, y luego sí hace polares.Espero ayude el comentario, cualquier cosa volvé a escribir nomás.
Saludos,
Leandro
