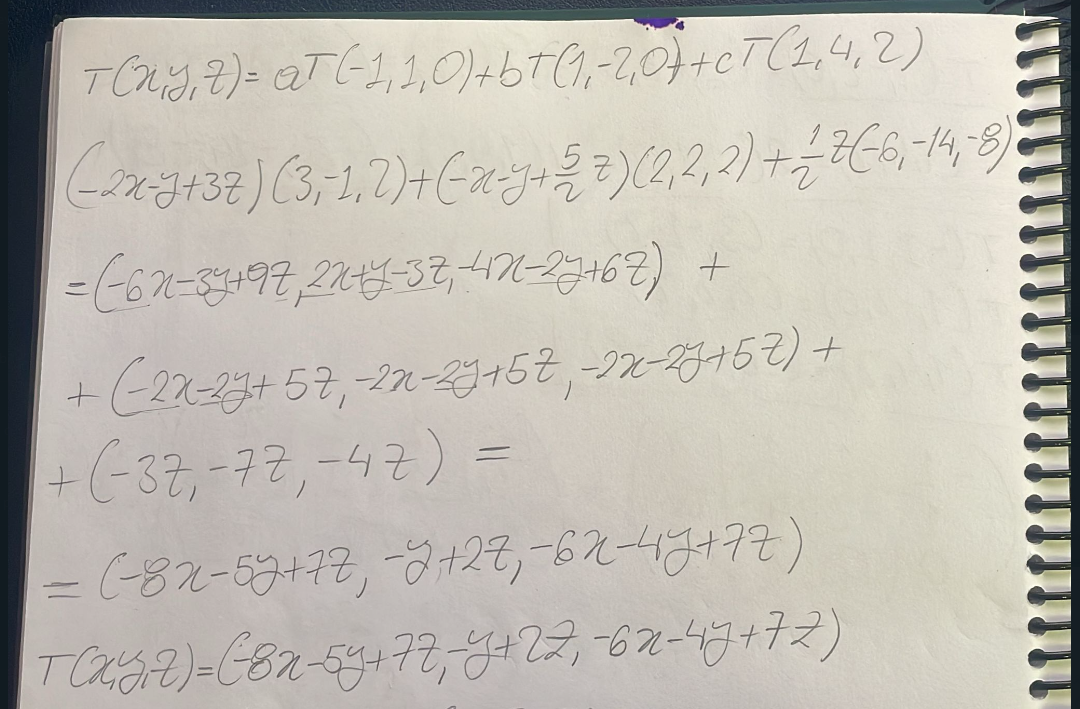Segundo Parcial 2008

Segundo Parcial 2008

de Alexis Sokorov Vargas -
Número de respuestas: 5

Buenas, tengo dudas sobre cómo resolver este ejercicio:


Me está pidiendo básicamente cómo es el núcleo e imagen de $$T$$, pero no tengo la expresión de la transformación.

Pensé en lo siguiente:

Me tomo un vector genérico $$(x,y,z) \in \mathbb{R} ^3 $$ que se pueda expresar como C.L. sobre los elementos de mi base $$A$$ No sé si eso está bien.

Por otra parte, hallé los transformados de los vectores de $$A$$ a través de la matriz asociada $$_A (T)_A$$ y me dio que $$T(-1,1,0)=(3,-1,2) ; T(1,-2,0)=(2,2,2) ; T(1,4,2)=(-6,-14,-8)$$

Y supongo que si hago $$T(x,y,z)=a T(-1,1,0) + b T(1,-2,0) + c T(1,4,2)$$ para poder hallar el transformado de mi $$T$$, no sé si es por ahí o pifié en algo
En respuesta a Alexis Sokorov Vargas

Re: Segundo Parcial 2008

de Victoria Garcia Tejera -
Hola, perfecto hallados los transformados de los elementos de la base. Recordar que esos transformados forman un generador de la imagen.

Pero sí, lo que planteás para expresar la transformación $$T$$ en un vector genérico (expresado en coordenadas de la base canónica), esta muy bien. Entiendo que a muchos les queda más cómodo tener la expresión general de la transformación para después trabajar con ella.
En respuesta a Victoria Garcia Tejera

Re: Segundo Parcial 2008

de Alexis Sokorov Vargas -
Claro, pero yo hice esto


Escribí a mi vector genérico $$(x,y,z)$$ como C.L. de los elementos de la base $$A$$ y llegué a esos escalares.
Traté de aplicar la linealidad por $$T$$ como mencioné anteriormente pero llegué a esto:



Se me hace un poco raro que me haya quedado $$T(x,y,z)=(-8x-5y+7z,-y+2z,-6x-4y+7z)$$ porque mi T.L. es $$T: \mathbb{R} ^3 \rightarrow \mathbb{R} ^3$$

Entonces ahí sí traté de calcular $$N(T)$$ pero me queda esto:



No es lo mismo, capaz derrapé en algo 
En respuesta a Alexis Sokorov Vargas

Re: Segundo Parcial 2008

de Victoria Garcia Tejera -
Hola, creo que el problema es que en las respuestas posibles, los vectores están expresados en coordenadas de la base $$A$$, y no de la canónica. Pienso que hubiera sido bueno que se aclare eso.

(La respuesta sería la E)
En respuesta a Alexis Sokorov Vargas

Re: Segundo Parcial 2008

de Juan Pablo Ponce Diaz -
claro el nucleo serian los vectores en origen que transformados dan el vector nulo.
entonces podes crear la base del nucleo igualando a cero la suma de todos los vectores de A transformados como ya los conseguiste.
luego ese vector que tenes como resultante es el nucleo y podrias ver cual es la respuesta correcta a partir de eso. ¿no?
y cuando transformas la base tambien obtenes un generador de la imagen

voy a hacerlo y ver si llego a alguna conclusion.
En respuesta a Alexis Sokorov Vargas

Re: Segundo Parcial 2008

de Juan Pablo Ponce Diaz -
Bueno repasando bastante y mirando el ultimo teorico en open.fing de 2019 entendi como se hace este ejercicio pero la verdad que es medio tricky.

estoy de acuerdo que es la opcion E .
1) cada columna de la matriz asociada son las coordenadas de los vectores de la base transformados. o sea que serian los vectores generadores de la imagen de T
2) como la base es la misma, salida y llegada no necesitas volver a "convertir" esos vectores mirando la base sino que directamente son los vectores del lado de llegada.

no necesitas multiplicar la matriz con los vectores, directamente tenes el generador de la imagen ahi y es LD por lo que escalerizando te das cuenta que el (2,0,4) Es combinación lineal de los otros 2 por lo que la base de la imagen es [(1,3,1),(0,1,1)]

Luego para obtener la base del nucleo usas una matriz ampleada.
La matriz asociada la amplias agregandole una columna de ceros y volves a escalerizar. el resultado de esa escalerización te da la relacion entre a,b y c para que T(a(-1,1,0) +b(1,-2,0) + c(1,4,2) ) = (0,0,0)
entonces obtenes que a = -2c, b= 6c para todo c . asi que ahi tienes el vector c(-2, 6 , 1) Que si te fijas es el generador del nucleo que aparece en las opciones D y E.

juntas toda esa información y la unica respuesta correcta es la E