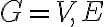Buenas!!
Estaba haciendo este ejercicio y me surgieron dudas de como hacerlo. Según entendí hasta ahora, debo resolver el problema de independent set usando el problema conjunto diverso transformando el problema original de forma polinomial.
Entonces me dan un grafo G=(V,E) y debo encontrar un independent set usando conjunto diverso, por lo que debería hacer la tabla A que usa este problema.
Primero pensé que a cada nodo lo considero un cliente y los uno si compraron algo en común. Pero luego al hacer la tabla llego al problema de que no sabría como "inventar" los productos ya que en el ejemplo que nos dan el grafo serían 3 nodos donde uno está conectado a los otros dos pero los otros dos entre ellos no, por lo que tendrían que haber más de un producto, y puedo hacer la tabla pero podría ser muy complicado ya que tendría que ver que coincida y no creo que sea así.
Alguna ayuda?
Gracias!!!!