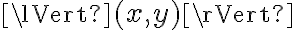Buenas noches, tengo una duda respecto a este ejercicio:
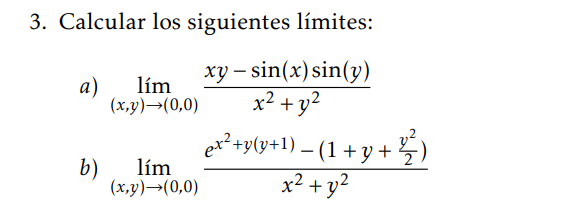
Quise ver si la composición me era más fácil para calcular el Taylor de 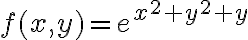 mediante
mediante 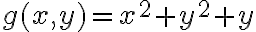 y
y 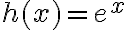
En el Taylor de 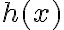 compondría con
compondría con 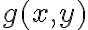 pero me quedaría lo siguiente (basándome en
pero me quedaría lo siguiente (basándome en 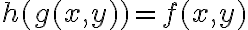 )
) 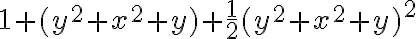
Porque el Taylor de 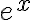 es
es 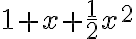 (en la
(en la  pongo el polinomio de
pongo el polinomio de  ) pero no sé si eso está bien y si sí, cómo sigo? Porque me quedaría un polinomio bastante largo con el último término al cuadrado y no sé qué descartarme para que me de un valor válido el límite
) pero no sé si eso está bien y si sí, cómo sigo? Porque me quedaría un polinomio bastante largo con el último término al cuadrado y no sé qué descartarme para que me de un valor válido el límite
Muestro cómo lo hice:

El desarrollo del cuadrado me dio con términos al cubo y a la cuarta (por eso me los descarté) pero me queda por ejemplo 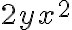 o
o 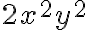 y no sé si también tengo que razonar igual
y no sé si también tengo que razonar igual