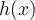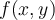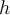Buenas noches hice el ejercicio pero no sé si está bien:

Hallé el Taylor de 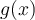 en
en 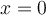 y me dio
y me dio 
En la parte de los diferenciales me dio que  y que
y que 
Pero el producto de los Taylor de una variable (descartando aquello que sea grado  ) me queda
) me queda 
¿Es eso el ejercicio o pifié en algo?