CriptoAp: Hash 1.4

1.4. Marca las palabras que entregan el tamaño del archivo (o texto) y comprueba que el valor en hexadecimal indicado es la cantidad de bits en decimal del mensaje

Entiendo lo siguiente:

M=Hola, buenos días. ¿Cómo estás? son 31 bytes = 248 bits

Después de realizar el hash, las 2 últimas palabras marcan el largo del mensaje y son:

Palabra 15 = 00011000000000010000000000000000

Palabra 16 = 00000000000000000000000000000000

Al pasar las 2 palabras a hexa obtengo

18 01 00 00 00 00 00 00

Estoy haciendo algo mal ? porque no me doy cuenta como llego a 248 bits ?

Re: Hash 1.4

de German Gustavo Bollmann - domingo, 5 de noviembre de 2023, 12:42

Les detallo el mensaje es

M=Hola, buenos días. ¿Cómo estás?

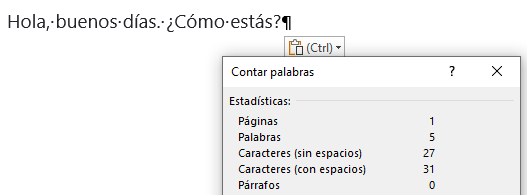
Que son 31 letras y símbolos, no lo hagan a mano usen el WORD por ejemplo (marcan el texto y hacen click en el pie de pagina donde dice palabras , a la izquierda de pagina.

Y les aparece algo como esto

Ok si tengo 31 elementos entonces si cada ascii vale 8 bits = 31 *8 = 248 bits del mensaje

Ahora bien MD5 procesa un bloque de 512 bits y lo divide en 16 palabras de 32 bits cada uno.

En MD5 las dos ultimas palabras están reservadas (últimos 64 bits). Ósea que los bits del bloque usable son 448bits (512 -64) =448 Bits

Tengo que completar el bloque , osea le pone un 1 y rellena con ceros.

Ahi me di cuenta que hay un bug con la herramienta y no esta mostrando bien lo valores del padding

Palabra 1 01100001011011000110111101001000 = 616C6F48

Palabra 2 01110101011000100010000000101100 = 7562202C

Palabra 3 01110011011011110110111001100101 = 736F6E65

Palabra 4 01100001111011010110010000100000 = 61ED6420

Palabra 5 10111111001000000010111001110011 = BF202E73

Palabra 6 01101111011011011111001101000011 = 6F6DF343

Palabra 7 01110100011100110110010100100000 = 74736520

Palabra 8 10000000001111110111001111100001 = 803F73E1 mensaje

Palabra 9 00000000000000000000000000000000 = 00000000

Palabra 10 00000000000000000000000000000000 = 00000000

Palabra 11 00000000000000000000000000000000 = 00000000

Palabra 12 00000000000000000000000000000000 = 00000000

Palabra 13 00000000000000000000000000000000 = 00000000

Palabra 14 00000000000000000000000000000000 = 00000000

Palabra 15 00000000000000000000000011111000 = 000000F8

Palabra 16 00000000000000000000000000000000 = 00000000

El bloque es de 248 bits que en HEXA es F8

Se cumple que Mensaje + Relleno + Tamaño = 512 bits

Les dejo el mismo bloque en SHA1 para que vean la diferencia

Las palabras del bloque 1 del mensaje son:

Palabra 1 01001000011011110110110001100001 = 486F6C61

Palabra 2 00101100001000000110001001110101 = 2C206275

Palabra 3 01100101011011100110111101110011 = 656E6F73

Palabra 4 00100000011001001110110101100001 = 2064ED61

Palabra 5 01110011001011100010000010111111 = 732E20BF

Palabra 6 01000011111100110110110101101111 = 43F36D6F

Palabra 7 00100000011001010111001101110100 = 20657374

Palabra 8 11100001011100110011111110000000 = E1733F80